| 某人投篮球3次,三次中能中一次的概率为,能中2次的概率为,能中3次的概率为,那么此人三次投篮都不中的概率为( ) |
相关习题
科目:高中数学
来源:2009-2010学年北京市通州区高二(上)期中数学试卷(必修3)(解析版)
题型:选择题
某人投篮球3次,三次中能中一次的概率为
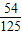
,能中2次的概率为
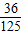
,能中3次的概率为

,那么此人三次投篮都不中的概率为( )
A.
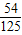
B.
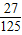
C.
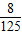
D.
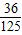
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
某人投篮球3次,三次中能中一次的概率为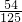 ,能中2次的概率为
,能中2次的概率为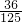 ,能中3次的概率为
,能中3次的概率为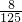 ,那么此人三次投篮都不中的概率为
,那么此人三次投篮都不中的概率为
- A.
- B.
- C.
- D.
查看答案和解析>>
科目:高中数学
来源:
题型:
在某校组织的一次篮球定点投篮训练中,规定每人最多投3次;在A处每次投进一球得3分,在B处每投进一球得2分,如果前两次得分之和超过3分即停止投篮,否则投第三次,某同学在A处的命中率q1为0.25,在B处的命中率为q2,该同学选择先在A处投一球,以后都在B处投,用ξ表示该同学投篮训练结束后所得的总分,ξ=0的概率为0.03.
(1)写出ξ值所有可能的值;
(2)求q2的值;
(3)求得到总分最大值的概率.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年北京市房山区高三(上)期末数学试卷(理科)(解析版)
题型:解答题
在某校组织的一次篮球定点投篮测试中,规定每人最多投3次.每次投篮的结果相互独立.在A处每投进一球得3分,在B处每投进一球得2分,否则得0分.将学生得分逐次累加并用ξ表示,如果ξ的值不低于3分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在A处投一球,以后都在B处投:方案2:都在B处投篮.甲同学在A处投篮的命中率为0.5,在B处投篮的命中率为0.8.
(1)当甲同学选择方案1时.
①求甲同学测试结束后所得总分等于4的概率:
②求甲同学测试结束后所得总分ξ的分布列和数学期望Eξ;
(2)你认为甲同学选择哪种方案通过测试的可能性更大?说明理由.
查看答案和解析>>
科目:高中数学
来源:2013年天津市南开区高考数学二模试卷(理科)(解析版)
题型:解答题
在某校组织的一次篮球定点投篮测试中,规定每人最多投3次.每次投篮的结果相互独立.在A处每投进一球得3分,在B处每投进一球得2分,否则得0分.将学生得分逐次累加并用ξ表示,如果ξ的值不低于3分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在A处投一球,以后都在B处投:方案2:都在B处投篮.甲同学在A处投篮的命中率为0.5,在B处投篮的命中率为0.8.
(1)当甲同学选择方案1时.
①求甲同学测试结束后所得总分等于4的概率:
②求甲同学测试结束后所得总分ξ的分布列和数学期望Eξ;
(2)你认为甲同学选择哪种方案通过测试的可能性更大?说明理由.
查看答案和解析>>
科目:高中数学
来源:2010-2011学年广西南宁二中高三(下)5月月考数学试卷(文科)(解析版)
题型:解答题
在某校组织的一次篮球定点投篮训练中,规定每人最多投3次;在A处每次投进一球得3分,在B处每投进一球得2分,如果前两次得分之和超过3分即停止投篮,否则投第三次,某同学在A处的命中率q1为0.25,在B处的命中率为q2,该同学选择先在A处投一球,以后都在B处投,用ξ表示该同学投篮训练结束后所得的总分,ξ=0的概率为0.03.
(1)写出ξ值所有可能的值;
(2)求q2的值;
(3)求得到总分最大值的概率.
查看答案和解析>>
科目:高中数学
来源:广西南宁二中2011届高三5月月考数学文综试题
题型:044
在某校组织的一次篮球定点投篮训练中,规定每人最多投3次;在A处每次投进一球得3分,在B处每投进一球得2分,如果前两次得分之和超过3分即停止投篮,否则投第三次,某同学在A处的命中率 ,在B处的命中率为q2,该同学选择先在A处投一球,以后都在B处投,用
,在B处的命中率为q2,该同学选择先在A处投一球,以后都在B处投,用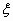 表示该同学投篮训练结束后所得的总分,
表示该同学投篮训练结束后所得的总分,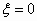 的概率为0.03.
的概率为0.03.
(1)写出 值所有可能的值;
值所有可能的值;
(2)求q2的值;
(3)求得到总分最大值的概率.
查看答案和解析>>
科目:高中数学
来源:
题型:
(2012•许昌三模)在某校篮球队的首轮选拔测试中,参加测试的五名同学的投篮命中率分别为
,
,
,
,
,每人均有10次投篮机会,至少投中六次才能晋级下一轮测试,假设每人每次投篮相互独立,则晋级下一轮的人数大约为( )
查看答案和解析>>
科目:高中数学
来源:
题型:
(2013•南开区二模)在某校组织的一次篮球定点投篮测试中,规定每人最多投3次.每次投篮的结果相互独立.在A处每投进一球得3分,在B处每投进一球得2分,否则得0分.将学生得分逐次累加并用ξ表示,如果ξ的值不低于3分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在A处投一球,以后都在B处投:方案2:都在B处投篮.甲同学在A处投篮的命中率为0.5,在B处投篮的命中率为0.8.
(1)当甲同学选择方案1时.
①求甲同学测试结束后所得总分等于4的概率:
②求甲同学测试结束后所得总分ξ的分布列和数学期望Eξ;
(2)你认为甲同学选择哪种方案通过测试的可能性更大?说明理由.
查看答案和解析>>
科目:高中数学
来源:
题型:
某人投篮球3次,三次中能中一次的概率为
,能中2次的概率为
,能中3次的概率为
,那么此人三次投篮都不中的概率为( )
查看答案和解析>>

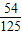 ,能中2次的概率为
,能中2次的概率为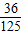 ,能中3次的概率为
,能中3次的概率为 ,那么此人三次投篮都不中的概率为( )
,那么此人三次投篮都不中的概率为( )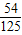
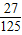
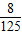
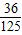
![]() ,在B处的命中率为q2,该同学选择先在A处投一球,以后都在B处投,用
,在B处的命中率为q2,该同学选择先在A处投一球,以后都在B处投,用![]() 表示该同学投篮训练结束后所得的总分,
表示该同学投篮训练结束后所得的总分,![]() 的概率为0.03.
的概率为0.03.![]() 值所有可能的值;
值所有可能的值;