
a,b,c三个整数满足a<b<c,则( )
|
科目:初中数学 来源:不详 题型:单选题
| A.a+c<b+c | B.|a|+|c|<|b|+|c| | C.ab<ac | D.|a||b|<|a||c| |
科目:初中数学 来源: 题型:
一个直角三角形三边的长a、b、c都是整数,且满足a<b<c,a+c=49.则这个直角三角形的面积( )
A、200 B、210 C、220 D、230[
科目:初中数学 来源:2012年浙江省宁波市小曹娥中学自主招生考试数学摸拟试卷(三)(解析版) 题型:选择题
 没有实数根,则满足条件的实数a的取值范围是0<a<1;
没有实数根,则满足条件的实数a的取值范围是0<a<1;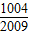 ;
;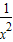 +
+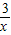 的最大值为2;
的最大值为2;科目:初中数学 来源: 题型:单选题
 没有实数根,则满足条件的实数a的取值范围是0<a<1;
没有实数根,则满足条件的实数a的取值范围是0<a<1; ;
;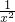 +
+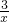 的最大值为2;
的最大值为2;科目:初中数学 来源:不详 题型:单选题
A.要使表达式
| ||||||||
B.满足不等式-
| ||||||||
C.当1,x,3分别为某个三角形的三边长时,有
| ||||||||
D.若实数a,b满足
|
科目:初中数学 来源: 题型:阅读理解
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 11 |
| 4 |
| 13 |
| 4 |
| 3 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
科目:初中数学 来源: 题型:填空题
科目:初中数学 来源:不详 题型:填空题
科目:初中数学 来源:第22章《二次根式》易错题集(03):22.1 二次根式(解析版) 题型:选择题
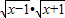 有意义,则x≥1
有意义,则x≥1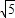 <x<
<x< 的整数x共有5个
的整数x共有5个 成立
成立 +|b-2|=0,则以a,b为边长的等腰三角形的周长为10
+|b-2|=0,则以a,b为边长的等腰三角形的周长为10湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com