设函数f(x)=sin(ωx+φ)(ω>0,0<φ<),若将f(x)的图象沿x轴向右平移个单位长度,得到的图象经过坐标原点;若将f(x)的图象上所有点的横坐标缩短到原来的倍(纵坐标不变),得到的图象关于直线x=对称.则( )| A.ω=π,φ= | B.ω=2π,φ= | C.ω=π,φ= | D.ω=3π,φ= |
|
相关习题
科目:高中数学
来源:
题型:
设函数f(x)=sin(ωx+φ)(
ω>0,0<φ<),若将f(x)的图象沿x轴向右平移
个单位长度,得到的图象经过坐标原点;若将f(x)的图象上所有点的横坐标缩短到原来的
倍(纵坐标不变),得到的图象关于直线
x=对称.则( )
| | | |
查看答案和解析>>
科目:高中数学
来源:
题型:
设函数f(x)=sin(ωx+φ)(ω>0,-
<φ<
),给出以下四个论断:
①f(x)的周期为π; ②f(x)在区间(-
,0)上是增函数;
③f(x)的图象关于点(
,0)对称;④f(x)的图象关于直线x=
对称.
以其中两个论断作为条件,另两个论断作为结论,写出你认为正确的一个命题:
⇒
(只需将命题的序号填在横线上).
查看答案和解析>>
科目:高中数学
来源:
题型:
设函数f(x)=sin(ωx+φ)(ω>0,
-<?<),给出以下四个论断:
①它的图象关于直线x=
对称;
②它的周期为π;
③它的图象关于点(
,0)对称;
④在区间[-
,0]上是增函数.
以其中两个论断作为条件,余下两个论断作为结论,写出你认为正确的两个命题:
(1)
①③⇒②④
①③⇒②④
; (2)
①②⇒③④
①②⇒③④
.
查看答案和解析>>
科目:高中数学
来源:
题型:
设函数f(x)=sin(ωx+?)(ω>0,
-<?<),给出以下四个论断:①它的图象关于直线
x=对称;②它的图象关于点(
,0)对称;③它的最小正周期是T=π;④它在区间
[-,0)上是增函数.
以其中的两个论断作为条件,余下的两个论断作为结论,写出你认为正确的两个命题,并对其中的一个命题加以证明.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年湖南省长沙市望城一中、长沙县实验中学高三(上)10月联考数学试卷(理科)(解析版)
题型:填空题
设函数f(x)=sin(ωx+φ)(ω>0,-

<φ<

),给出以下四个论断:
①f(x)的周期为π; ②f(x)在区间(-

,0)上是增函数;
③f(x)的图象关于点(

,0)对称;④f(x)的图象关于直线x=

对称.
以其中两个论断作为条件,另两个论断作为结论,写出你认为正确的一个命题:
⇒
(只需将命题的序号填在横线上).
查看答案和解析>>
科目:高中数学
来源:2012-2013学年江苏省淮安市金湖中学高三(上)期末数学试卷(解析版)
题型:填空题
设函数f(x)=sin(ωx+φ)(ω>0,-

<φ<

),给出以下四个论断:
①f(x)的周期为π; ②f(x)在区间(-

,0)上是增函数;
③f(x)的图象关于点(

,0)对称;④f(x)的图象关于直线x=

对称.
以其中两个论断作为条件,另两个论断作为结论,写出你认为正确的一个命题:
⇒
(只需将命题的序号填在横线上).
查看答案和解析>>
科目:高中数学
来源:2012-2013学年湖南省望城一中、长沙县实验中学高三(上)10月联考数学试卷(理科)(解析版)
题型:填空题
设函数f(x)=sin(ωx+φ)(ω>0,-

<φ<

),给出以下四个论断:
①f(x)的周期为π; ②f(x)在区间(-

,0)上是增函数;
③f(x)的图象关于点(

,0)对称;④f(x)的图象关于直线x=

对称.
以其中两个论断作为条件,另两个论断作为结论,写出你认为正确的一个命题:
⇒
(只需将命题的序号填在横线上).
查看答案和解析>>
科目:高中数学
来源:2011-2012学年江苏省苏州市吴中区苏苑中学高一(上)12月月考数学试卷(解析版)
题型:填空题
设函数f(x)=sin(ωx+φ)(ω>0,

),给出以下四个论断:
①它的图象关于直线x=

对称;
②它的周期为π;
③它的图象关于点(

,0)对称;
④在区间[-

,0]上是增函数.
以其中两个论断作为条件,余下两个论断作为结论,写出你认为正确的两个命题:
(1)
; (2)
.
查看答案和解析>>
科目:高中数学
来源:2010-2011学年福建省莆田四中高一(下)期末数学试卷(理科)(必修4、5)(解析版)
题型:填空题
设函数f(x)=sin(ωx+φ)(ω>0,
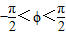
),给出以下四个论断:
①它的图象关于直线x=

对称;
②它的周期为π;
③它的图象关于点(

,0)对称;
④在区间[-

,0]上是增函数.
以其中两个论断作为条件,余下两个论断作为结论,写出你认为正确的两个命题:
(1)
; (2)
.
查看答案和解析>>
科目:高中数学
来源:2009-2010学年山东省日照市实验高中高一(下)期末数学练习试卷7(必修3、4)(解析版)
题型:填空题
设函数f(x)=sin(ωx+φ)(ω>0,

),给出以下四个论断:
①它的图象关于直线x=

对称;
②它的周期为π;
③它的图象关于点(

,0)对称;
④在区间[-

,0]上是增函数.
以其中两个论断作为条件,余下两个论断作为结论,写出你认为正确的两个命题:
(1)
; (2)
.
查看答案和解析>>

 <φ<
<φ< ),给出以下四个论断:
),给出以下四个论断: ,0)上是增函数;
,0)上是增函数; ,0)对称;④f(x)的图象关于直线x=
,0)对称;④f(x)的图象关于直线x= 对称.
对称. <φ<
<φ< ),给出以下四个论断:
),给出以下四个论断: ,0)上是增函数;
,0)上是增函数; ,0)对称;④f(x)的图象关于直线x=
,0)对称;④f(x)的图象关于直线x= 对称.
对称. <φ<
<φ< ),给出以下四个论断:
),给出以下四个论断: ,0)上是增函数;
,0)上是增函数; ,0)对称;④f(x)的图象关于直线x=
,0)对称;④f(x)的图象关于直线x= 对称.
对称. ),给出以下四个论断:
),给出以下四个论断: 对称;
对称;  ,0)对称;
,0)对称;  ,0]上是增函数.
,0]上是增函数.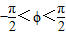 ),给出以下四个论断:
),给出以下四个论断: 对称;
对称;  ,0)对称;
,0)对称;  ,0]上是增函数.
,0]上是增函数. ),给出以下四个论断:
),给出以下四个论断: 对称;
对称;  ,0)对称;
,0)对称;  ,0]上是增函数.
,0]上是增函数.