
已知θ是三角形中的一个最小内角,且acos2
|
科目:高中数学 来源: 题型:
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| A、a<-1 | B、a>-1 |
| C、a≤-3 | D、a≥-3 |
科目:高中数学 来源:不详 题型:单选题
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| A.a<-1 | B.a>-1 | C.a≤-3 | D.a≥-3 |
科目:高中数学 来源:《第3章 三角恒等变换》2011年单元测试卷(解析版) 题型:选择题
 ,则a的取值范围是( )
,则a的取值范围是( )科目:高中数学 来源: 题型:
| CE |
| CF |
科目:高中数学 来源:辽宁省高考真题 题型:解答题
 的最大值和最小值。
的最大值和最小值。科目:高中数学 来源:辽宁省高考真题 题型:解答题
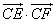 的最大值和最小值。
的最大值和最小值。科目:高中数学 来源:2007年普通高等学校招生全国统一考试、理科数学(辽宁卷) 题型:044
已知正三角形OAB的三个顶点都在抛物线y2=2x上,其中O为坐标原点,设圆C是OAB的内接圆(点C为圆心)
(Ⅰ)求圆C的方程;
(Ⅱ)设圆M的方程为(x-4-7cosθ)2+(y-7cosθ)2=1,过圆M上任意一点P分别作圆C的两条切线PE,PF,切点为E,F,求![]() 的最大值和最小值.
的最大值和最小值.
科目:高中数学 来源:2007年普通高等学校招生全国统一考试 文科数学(辽宁) 题型:044
已知正三角形OAB的三个顶点都在抛物线y2=2x上,其中O为坐标原点,设圆C是△OAB的内接圆(点C为圆心)
(I)求圆C的方程;
(II)设圆M的方程为![]() ,过圆M上任意一点P分别作圆C的两条切线PE,PF,切点为E,F,求
,过圆M上任意一点P分别作圆C的两条切线PE,PF,切点为E,F,求![]() 的最大值和最小值.
的最大值和最小值.
科目:高中数学 来源:2012-2013学年福建省高三第一次阶段考试文科数学试卷(解析版) 题型:填空题
已知下列结论:
①已知 为实数,则“
为实数,则“ ”是“
”是“ 成等比数列”的充要条件;
成等比数列”的充要条件;
②满足条件 的△ABC的个数为2;
的△ABC的个数为2;
③若两向量 的夹角为钝角,则实数
的夹角为钝角,则实数 的取值范围
的取值范围
为 ;
;
④若 为三角形中的最小内角,则函数
为三角形中的最小内角,则函数 的值域是
的值域是 ;
;
⑤某厂去年12月份产值是同年一月份产值的m倍,则该厂去年的月平均增长率
为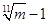 ;
;
则其中正确结论的序号是__________;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com