
平面直角坐标系内与点(3,-5)关于y轴对称的点的坐标是( )
|
科目:初中数学 来源: 题型:
| 2 |
| 3 |
| 2 |
| 3 |
| S1 |
| S2 |
 ,并写出自变量x的取值范围.
,并写出自变量x的取值范围.科目:初中数学 来源: 题型:解答题
 x+1,如果将坐标纸折叠,使直线l1与l2重合,此时点(-2,0)与点(0,2)也重合.
x+1,如果将坐标纸折叠,使直线l1与l2重合,此时点(-2,0)与点(0,2)也重合. )为圆心,CA的长为半径作圆,过点B任作一条直线(不与y轴重合),与⊙C相交于D、E两点(点D在点E的下方)
)为圆心,CA的长为半径作圆,过点B任作一条直线(不与y轴重合),与⊙C相交于D、E两点(点D在点E的下方)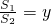 ,求y与x之间的函数关系式
,求y与x之间的函数关系式 ,并写出自变量x的取值范围.
,并写出自变量x的取值范围.科目:初中数学 来源:不详 题型:解答题
| 2 |
| 3 |
| 2 |
| 3 |
| S1 |
| S2 |
 ,并写出自变量x的取值范围.
,并写出自变量x的取值范围.科目:初中数学 来源:2011-2012学年云南省西双版纳州勐海县打洛镇中学九年级(上)第二次月考数学试卷(解析版) 题型:填空题
科目:初中数学 来源:2011-2012学年新人教版九年级(上)期末数学复习试卷(一)(解析版) 题型:填空题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com