
若a,b,c为三角形三边,则关于的二次方程
|
科目:初中数学 来源: 题型:
| 2 |
| 2 |
| A、15° | B、30° |
| C、45° | D、60° |
科目:初中数学 来源: 题型:
若![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的两个根,则方程的两个根
的两个根,则方程的两个根![]() 和系数
和系数![]() 有如下关系:
有如下关系:![]() . 我们把它们称为根与系数关系定理. 如果设二次函数
. 我们把它们称为根与系数关系定理. 如果设二次函数![]() 的图象与x轴的两个交点为
的图象与x轴的两个交点为![]() .利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
.利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
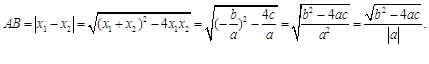
请你参考以上定理和结论,解答下列问题:
设二次函数![]() 的图象与x轴的两个交点为
的图象与x轴的两个交点为![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,显然
,显然![]() 为等腰三角形.
为等腰三角形.
(1)当![]() 为等腰直角三角形时,求
为等腰直角三角形时,求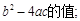
(2)当![]() 为等边三角形时,求
为等边三角形时,求![]()
科目:初中数学 来源: 题型:
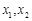 是关于
是关于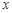 的一元二次方程
的一元二次方程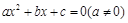 的两个根,则方程的两个根
的两个根,则方程的两个根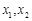 和系数
和系数 有如下关系:
有如下关系: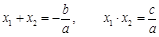 . 我们把它们称为根与系数关系定理. 如果设二次函数
. 我们把它们称为根与系数关系定理. 如果设二次函数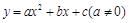 的图象与x轴的两个交点为
的图象与x轴的两个交点为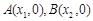 .利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
.利用根与系数关系定理我们又可以得到A、B两个交点间的距离为: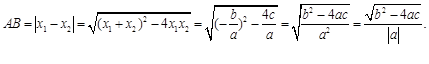
 的图象与x轴的两个交点为
的图象与x轴的两个交点为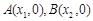 ,抛物线的顶点为
,抛物线的顶点为 ,显然
,显然 为等腰三角形.
为等腰三角形. 为等腰直角三角形时,求
为等腰直角三角形时,求
 为等边三角形时,求
为等边三角形时,求
科目:初中数学 来源:2012届广东省汕头市濠江区中考模拟考试数学卷(带解析) 题型:解答题
若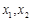 是关于
是关于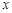 的一元二次方程
的一元二次方程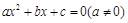 的两个根,则方程的两个根
的两个根,则方程的两个根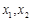 和系数
和系数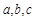 有如下关系:
有如下关系: . 我们把它们称为根与系数关系定理. 如果设二次函数
. 我们把它们称为根与系数关系定理. 如果设二次函数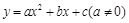 的图象与x轴的两个交点为
的图象与x轴的两个交点为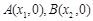 .利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
.利用根与系数关系定理我们又可以得到A、B两个交点间的距离为: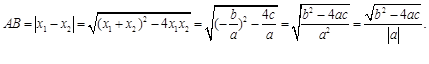
请你参考以上定理和结论,解答下列问题:
设二次函数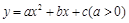 的图象与x轴的两个交点为
的图象与x轴的两个交点为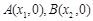 ,抛物线的顶点为
,抛物线的顶点为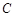 ,显然
,显然 为等腰三角形.
为等腰三角形.
(1)当 为等腰直角三角形时,求
为等腰直角三角形时,求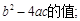
(2)当 为等边三角形时,求
为等边三角形时,求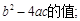
科目:初中数学 来源:2011-2012学年广东省汕头市濠江区中考模拟考试数学卷(解析版) 题型:解答题
若 是关于
是关于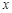 的一元二次方程
的一元二次方程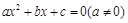 的两个根,则方程的两个根
的两个根,则方程的两个根 和系数
和系数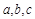 有如下关系:
有如下关系: .
我们把它们称为根与系数关系定理. 如果设二次函数
.
我们把它们称为根与系数关系定理. 如果设二次函数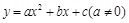 的图象与x轴的两个交点为
的图象与x轴的两个交点为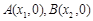 .利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
.利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
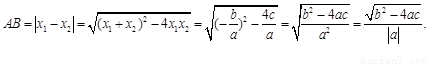
请你参考以上定理和结论,解答下列问题:
设二次函数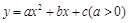 的图象与x轴的两个交点为
的图象与x轴的两个交点为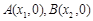 ,抛物线的顶点为
,抛物线的顶点为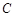 ,显然
,显然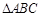 为等腰三角形.
为等腰三角形.
(1)当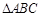 为等腰直角三角形时,求
为等腰直角三角形时,求
(2)当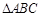 为等边三角形时,求
为等边三角形时,求
科目:初中数学 来源:河北 题型:单选题
| 2 |
| 2 |
| A.15° | B.30° | C.45° | D.60° |
科目:初中数学 来源: 题型:
若![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的两个根,则方程的两个根
的两个根,则方程的两个根![]() 和系数
和系数![]() 有如下关系:
有如下关系:![]() . 我们把它们称为根与系数关系定理.
. 我们把它们称为根与系数关系定理.
如果设二次函数![]() 的图象与x轴的两个交点为
的图象与x轴的两个交点为![]() .利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:
.利用根与系数关系定理我们又可以得到A、B两个交点间的距离为:

请你参考以上定理和结论,解答下列问题:
设二次函数![]() 的图象与x轴的两个交点为
的图象与x轴的两个交点为![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,显然
,显然![]() 为等腰三角形.
为等腰三角形.
(1)当![]() 为等腰直角三角形时,求
为等腰直角三角形时,求![]()
(2)当![]() 为等边三角形时,求
为等边三角形时,求![]()
科目:初中数学 来源:第1章《直角三角形的边角关系》好题集(05):6.2 特殊角的三角函数值(解析版) 题型:选择题
 的两根之差为
的两根之差为 ,则等腰三角形的一个底角是( )
,则等腰三角形的一个底角是( )科目:初中数学 来源:第7章《锐角三角函数》好题集(06):7.3 特殊角的三角函数(解析版) 题型:选择题
 的两根之差为
的两根之差为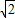 ,则等腰三角形的一个底角是( )
,则等腰三角形的一个底角是( )科目:初中数学 来源:第1章《解直角三角形》好题集(01):1.1 锐角三角函数(解析版) 题型:选择题
 的两根之差为
的两根之差为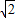 ,则等腰三角形的一个底角是( )
,则等腰三角形的一个底角是( )湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com