定义域为(0,+∞)的可导函数f(x)满足xf′(x)>f(x)且f(2)=0,则<0的解集为( )| A.(0,2) | B.(2,+∞) | C.(0,2)∪(2,+∞) | D.(0,+∞) |
|
相关习题
科目:高中数学
来源:
题型:
定义域为(0,+∞)的可导函数f(x)满足xf′(x)>f(x)且f(2)=0,则
<0的解集为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
定义域为(0,+∞)的可导函数f(x)满足xf′(x)>f(x)且f(2)=0,则
<0的解集为( )
| A.(0,2) | B.(2,+∞) | C.(0,2)∪(2,+∞) | D.(0,+∞) |
查看答案和解析>>
科目:高中数学
来源:2010-2011学年黑龙江省鹤岗一中高二(下)期末数学试卷(理科)(解析版)
题型:选择题
定义域为(0,+∞)的可导函数f(x)满足xf′(x)>f(x)且f(2)=0,则
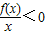
的解集为( )
A.(0,2)
B.(2,+∞)
C.(0,2)∪(2,+∞)
D.(0,+∞)
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
定义域为(0,+∞)的可导函数f(x)满足xf′(x)>f(x)且f(2)=0,则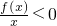 的解集为
的解集为
- A.
(0,2)
- B.
(2,+∞)
- C.
(0,2)∪(2,+∞)
- D.
(0,+∞)
查看答案和解析>>
科目:高中数学
来源:
题型:
已知可导函数f(x)为定义域上的奇函数,f(1)=1,f(2)=2.当x>0时,有3f(x)-x•f'(x)>1,则f(
-)的取值范围为( )
| | | |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知可导函数f(x)为定义域上的奇函数,f(1)=1,f(2)=2.当x>0时,有3f(x)-x•f'(x)>1,则f(
-)的取值范围为( )
| A.(,) | B.(-,-) | C.(-8,-1) | D.(4,8) |
查看答案和解析>>
科目:高中数学
来源:无为县模拟
题型:单选题
函数f(x)是定义域为R的可导函数,且对任意实数x都有f(x)=f(2-x)成立.若当x≠1时,不等式(x-1)•f′(x)<0成立,设a=f(0.5),
b=f(),c=f(3),则a,b,c的大小关系是( )
| A.b>a>c | B.a>b>c | C.c>b>a | D.a>c>b |
查看答案和解析>>
科目:高中数学
来源:2012-2013学年北京市朝阳区高三(上)期中数学试卷(理科)(解析版)
题型:选择题
函数f(x)是定义域为R的可导函数,且对任意实数x都有f(x)=f(2-x)成立.若当x≠1时,不等式(x-1)•f′(x)<0成立,设a=f(0.5),

,c=f(3),则a,b,c的大小关系是( )
A.b>a>c
B.a>b>c
C.c>b>a
D.a>c>b
查看答案和解析>>
科目:高中数学
来源:2013-2014学年湖北省荆门市龙泉中学高三(上)8月月考数学试卷(理科)(解析版)
题型:选择题
函数f(x)是定义域为R的可导函数,且对任意实数x都有f(x)=f(2-x)成立.若当x≠1时,不等式(x-1)•f′(x)<0成立,设a=f(0.5),

,c=f(3),则a,b,c的大小关系是( )
A.b>a>c
B.a>b>c
C.c>b>a
D.a>c>b
查看答案和解析>>
科目:高中数学
来源:2012-2013学年重庆市西南大学附中高二(下)期中数学试卷(理科)(解析版)
题型:选择题
已知可导函数f(x)为定义域上的奇函数,f(1)=1,f(2)=2.当x>0时,有3f(x)-x•f'(x)>1,则f(

)的取值范围为( )
A.(

,
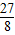
)
B.(

,

)
C.(-8,-1)
D.(4,8)
查看答案和解析>>

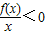 的解集为( )
的解集为( )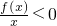 的解集为
的解集为 ,c=f(3),则a,b,c的大小关系是( )
,c=f(3),则a,b,c的大小关系是( ) ,c=f(3),则a,b,c的大小关系是( )
,c=f(3),则a,b,c的大小关系是( ) )的取值范围为( )
)的取值范围为( ) ,
,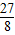 )
) ,
, )
)