
坐标平面上,有一线性函数过(-3,4)和(-7,4)两点,判断此函数图形会过哪两象限?( )
|
科目:初中数学 来源:台湾 题型:单选题
| A.第一象限和第二象限 | B.第一象限和第四象限 |
| C.第二象限和第三象限 | D.第二象限和第四象限 |
科目:初中数学 来源:2013年台湾省中考数学试卷(解析版) 题型:选择题
科目:初中数学 来源: 题型:单选题
科目:初中数学 来源: 题型:
如图:在平面直角坐标系中,将长方形纸片ABCD的顶点B与原点O重合,BC边放在x轴的正半轴上,AB=3,AD=6,将纸片沿过点M的直线折叠(点M在边AB上),使点B落在边AD上的E处(若折痕MN与x轴相交时,其交点即为N),过点E作EQ⊥BC于Q,交折痕于点P。
1.①当点 分别与AB的中点、A点重合时,那么对应的点P分别是点
分别与AB的中点、A点重合时,那么对应的点P分别是点![]() 、
、![]() ,则
,则![]() ( , )、
( , )、![]() ( , );②当∠OMN=60°时,对应的点P是点
( , );②当∠OMN=60°时,对应的点P是点![]() ,求
,求![]() 的坐标;
的坐标;
2.若抛物线![]() ,是经过(1)中的点
,是经过(1)中的点![]() 、
、![]() 、
、![]() ,试求a、b、c的值;
,试求a、b、c的值;
3.在一般情况下,设P点坐标是(x,y),那么y与x之间函数关系式还会与(2)中函数关系相同吗(不考虑x的取值范围)?请你利用有关几何性质(即不再用![]() 、
、![]() 、
、![]() 三点)求出y与x之间的关系来给予说明.
三点)求出y与x之间的关系来给予说明.
科目:初中数学 来源: 题型:
 分别与AB的中点、A点重合时,那么对应的点P分别是点
分别与AB的中点、A点重合时,那么对应的点P分别是点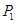 、
、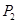 ,则
,则 ( , )、
( , )、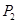 ( , );②当∠OMN=60°时,对应的点P是点
( , );②当∠OMN=60°时,对应的点P是点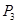 ,求
,求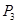 的坐标;
的坐标;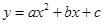 ,是经过(1)中的点
,是经过(1)中的点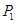 、
、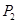 、
、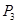 ,试求a、b、c的值;
,试求a、b、c的值;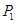 、
、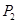 、
、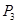 三点)求出y与x之间的关系来给予说明.
三点)求出y与x之间的关系来给予说明.科目:初中数学 来源:2012届江西省南昌市九年级下学期4月考数学卷(带解析) 题型:解答题
如图:在平面直角坐标系中,将长方形纸片ABCD的顶点B与原点O重合,BC边放在x轴的正半轴上,AB=3,AD=6,将纸片沿过点M的直线折叠(点M在边AB上),使点B落在边AD上的E处(若折痕MN与x轴相交时,其交点即为N),过点E作EQ⊥BC于Q,交折痕于点P。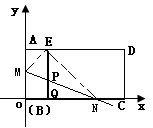
(1)①当点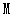 分别与AB的中点、A点重合时,那么对应的点P分别是点
分别与AB的中点、A点重合时,那么对应的点P分别是点 、
、 ,则
,则 ( , )、
( , )、 ( , );②当∠OMN=60°时,对应的点P是点
( , );②当∠OMN=60°时,对应的点P是点 ,求
,求 的坐标;
的坐标;
(2)若抛物线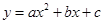 ,是经过(1)中的点
,是经过(1)中的点 、
、 、
、 ,试求a、b、c的值;
,试求a、b、c的值;
(3)在一般情况下,设P点坐标是(x,y),那么y与x之间函数关系式还会与(2)中函数关系相同吗(不考虑x的取值范围)?请你利用有关几何性质(即不再用 、
、 、
、 三点)求出y与x之间的关系来给予说明.
三点)求出y与x之间的关系来给予说明.
科目:初中数学 来源:2012届江西省南昌市九年级下学期第二次联考数学试卷(带解析) 题型:解答题
如图:在平面直角坐标系中,将长方形纸片ABCD的顶点B与原点O重合,BC边放在x轴的正半轴上,AB=3,AD=6,将纸片沿过点M的直线折叠(点M在边AB上),使点B落在边AD上的E处(若折痕MN与x轴相交时,其交点即为N),过点E作EQ⊥BC于Q,交折痕于点P。
【小题1】①当点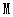 分别与AB的中点、A点重合时,那么对应的点P分别是点
分别与AB的中点、A点重合时,那么对应的点P分别是点 、
、 ,则
,则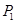 ( , )、
( , )、 ( , );②当∠OMN=60°时,对应的点P是点
( , );②当∠OMN=60°时,对应的点P是点 ,求
,求 的坐标;
的坐标;
【小题2】若抛物线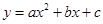 ,是经过(1)中的点
,是经过(1)中的点 、
、 、
、 ,试求a、b、c的值;
,试求a、b、c的值;
【小题3】在一般情况下,设P点坐标是(x,y),那么y与x之间函数关系式还会与(2)中函数关系相同吗(不考虑x的取值范围)?请你利用有关几何性质(即不再用 、
、 、
、 三点)求出y与x之间的关系来给予说明.
三点)求出y与x之间的关系来给予说明.
科目:初中数学 来源:2012年福建省漳州市中考数学二模试卷 (解析版) 题型:解答题

科目:初中数学 来源:2012年江西省南昌市十五校第二次联考初三数学试卷(解析版) 题型:解答题

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com