练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知以（-1，0）为圆心，1为半径的⊙M和抛物线y=x2+6x+11，现有两个命题：
    （1）抛物线y=x2+6x+11与⊙M没有交点；
    （2）将抛物线y=x2+6x+11向下平移3个单位，则此抛物线与⊙M相交．
    则以下结论正确的是（　　）
    A．只有命题（1）正确B．只有命题（2）正确
    C．命题（1），（2）都正确D．命题（1），（2）都不正确
    C
    请在这里输入关键词：
    相关习题

    科目：初中数学 来源：《第2章 二次函数》2009年单元水平测试（3）（解析版） 题型：选择题

    已知以（-1，0）为圆心，1为半径的⊙M和抛物线y=x2+6x+11，现有两个命题：
    （1）抛物线y=x2+6x+11与⊙M没有交点；
    （2）将抛物线y=x2+6x+11向下平移3个单位，则此抛物线与⊙M相交．
    则以下结论正确的是（ ）
    A．只有命题（1）正确
    B．只有命题（2）正确
    C．命题（1），（2）都正确
    D．命题（1），（2）都不正确

    查看答案和解析>>

    科目：初中数学 来源： 题型：单选题

    已知以（-1，0）为圆心，1为半径的⊙M和抛物线y=x2+6x+11，现有两个命题：
    （1）抛物线y=x2+6x+11与⊙M没有交点；
    （2）将抛物线y=x2+6x+11向下平移3个单位，则此抛物线与⊙M相交．
    则以下结论正确的是


    1. A.
      只有命题（1）正确
    2. B.
      只有命题（2）正确
    3. C.
      命题（1），（2）都正确
    4. D.
      命题（1），（2）都不正确

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网已知平面直角坐标系内，一次函数y=kx+2的图象与x轴相交于点A(-2
    		3
    ，0)    ，与y轴相交于点B．
    （1）求一次函数的解析式，并在直角坐标系中画出它的图象；
    （2）若以原点O为圆心的⊙O与直线AB相切于点C，求⊙O的半径和点C的坐标；
    （3）在x轴上是否存在点P，使△PAB为等腰三角形？若存在，请写出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知一直角三角形两直角边的长分别是3cm和4cm，以直角顶点为圆心，2.4cm长为半径作⊙O，则⊙O与斜边的位置关系是（　　）
    A、相交B、相切C、相离D、以上都不对

    查看答案和解析>>

    科目：初中数学 来源： 题型：

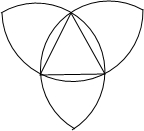    精英家教网已知一个等边三角形的边长为2，分别以它的三个顶点为圆心，边长为半径画弧，得到右图，那么图中所有的弧长的和是（　　）
    A、4πB、6πC、8πD、10π

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：如图所示，直线l的解析式为y=
    34
    x-3，并且与x轴、y轴分别相交于点A、B．
    （1）求A、B两点的坐标；
    （2）一个圆心在坐标原点、半径为1的圆，以0.4个单位/每秒的速度向x轴正方向运动，问什么时刻该圆与直线l相切；
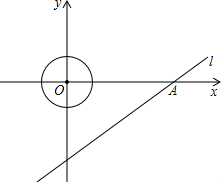    （3）在题（2）中，若在圆开始运动的同时，一动点P从B点出发，沿BA方向以0精英家教网.5个单位/秒的速度运动，问在整个运动的过程中，点P在动圆的园面（圆上和圆的内部）上一共运动了多长时间？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：矩形ABCD的面积为12，边AB与BC的长是关于x的方程x2-（m-5）x+m=0的两个根．
    （1）分别求出边AB和BC的长度；
    （2）以点A为圆心，AB长为半径画弧，交射线AD于点E，求四边形ABCE的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

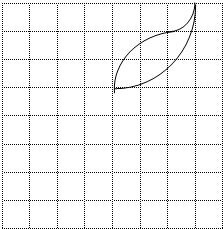    已知每个网格中小正方形的边长都是1，图中的图案是由三段以格点（每个小正精英家教网方形的顶点叫格点）为圆心，半径分别为1、2、3的圆弧围成．
    （1）填空：图中三段圆弧所围成的封闭图形的面积是
     
    （结果保留π）；
    （2）请你在图中以（1）中的图为基本图案，借助轴对称变换和旋转变换设计一个完整的图案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

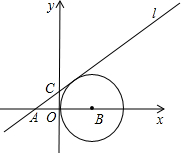    已知：如图，在平面直角坐标系中，点B在x轴上，以3为半径的⊙B与y轴相切，直线l过点A（-2，精英家教网0），且和⊙B相切，与y轴相交于点C．
    （1）求直线l的解析式；
    （2）若抛物线y=ax2+bx+c（a＞0）经过点O和B，顶点在⊙B上，求抛物线的解析式；
    （3）若点E在直线l上，且以A为圆心，AE为半径的圆与⊙B相切，求点E的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知对称轴为y轴的抛物线y=ax2+c，与直线l1交于A（-4，3）、B（2，0）两点．经过点C（0，-2）的直线l2与x轴平行，O为坐标原点．
    （Ⅰ）求直线l1和这条抛物线的解析式；
    （Ⅱ）以A为圆心，AO为半径的圆记为⊙A，判断直线l2与⊙A的位置关系，并说明理由；
    （Ⅲ）设直线l1上的点D的横坐标为-1，P（m，n）是（Ⅰ）中抛物线上的动点，当△PDO的周长最小时，求四边形CODP的面积．

    查看答案和解析>>


    同步练习册答案