| 在平面直角坐标系内,点P(x-2,2x-1)在第二象限,则x的取值范围是( ) |
相关习题
科目:初中数学
来源:
题型:
在平面直角坐标系内,点P(x-2,2x-1)在第二象限,则x的取值范围是( )
查看答案和解析>>
科目:初中数学
来源:不详
题型:单选题
在平面直角坐标系内,点P(x-2,2x-1)在第二象限,则x的取值范围是( )
查看答案和解析>>
科目:初中数学
来源:
题型:单选题
在平面直角坐标系内,点P(x-2,2x-1)在第二象限,则x的取值范围是
- A.
x<2
- B.
- C.
- D.
查看答案和解析>>
科目:初中数学
来源:
题型:解答题
 在平面直角坐标系内有两点A(-2,0),B(
在平面直角坐标系内有两点A(-2,0),B( ,0),CB所在直线为y=2x+b,
,0),CB所在直线为y=2x+b,
(1)求b与C的坐标;
(2)连接AC,求证:△AOC∽△COB;
(3)求过A,B,C三点且对称轴平行于y轴的抛物线解析式;
(4)在抛物线上是否存在一点P(不与C重合),使得S△ABP=S△ABC?若存在,请求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学
来源:湖南省中考真题
题型:解答题
在平面直角坐标系内有两点A(-2,0),B(
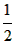
,0),CB所在直线为y=2x+b。
(1)求b与C的坐标;
(2)连接AC,求证:△AOC∽△COB;
(3)求过A,B,C三点且对称轴平行于y轴的抛物线解析式;
(4)在抛物线上是否存在一点P(不与C重合),使得S△ABP=S△ABC?若存在,请求出P点坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学
来源:第2章《二次函数》中考题集(41):2.7 最大面积是多少(解析版)
题型:解答题
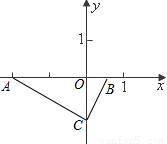
在平面直角坐标系内有两点A(-2,0),B(

,0),CB所在直线为y=2x+b,
(1)求b与C的坐标;
(2)连接AC,求证:△AOC∽△COB;
(3)求过A,B,C三点且对称轴平行于y轴的抛物线解析式;
(4)在抛物线上是否存在一点P(不与C重合),使得S
△ABP=S
△ABC?若存在,请求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学
来源:第34章《二次函数》中考题集(44):34.4 二次函数的应用(解析版)
题型:解答题
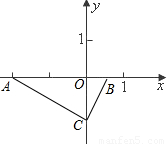
在平面直角坐标系内有两点A(-2,0),B(

,0),CB所在直线为y=2x+b,
(1)求b与C的坐标;
(2)连接AC,求证:△AOC∽△COB;
(3)求过A,B,C三点且对称轴平行于y轴的抛物线解析式;
(4)在抛物线上是否存在一点P(不与C重合),使得S
△ABP=S
△ABC?若存在,请求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学
来源:第2章《二次函数》中考题集(43):2.3 二次函数的应用(解析版)
题型:解答题
在平面直角坐标系内有两点A(-2,0),B(

,0),CB所在直线为y=2x+b,
(1)求b与C的坐标;
(2)连接AC,求证:△AOC∽△COB;
(3)求过A,B,C三点且对称轴平行于y轴的抛物线解析式;
(4)在抛物线上是否存在一点P(不与C重合),使得S
△ABP=S
△ABC?若存在,请求出P点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学
来源:第26章《二次函数》中考题集(41):26.3 实际问题与二次函数(解析版)
题型:解答题
在平面直角坐标系内有两点A(-2,0),B(

,0),CB所在直线为y=2x+b,
(1)求b与C的坐标;
(2)连接AC,求证:△AOC∽△COB;
(3)求过A,B,C三点且对称轴平行于y轴的抛物线解析式;
(4)在抛物线上是否存在一点P(不与C重合),使得S
△ABP=S
△ABC?若存在,请求出P点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学
来源:第2章《二次函数》中考题集(45):2.8 二次函数的应用(解析版)
题型:解答题
在平面直角坐标系内有两点A(-2,0),B(

,0),CB所在直线为y=2x+b,
(1)求b与C的坐标;
(2)连接AC,求证:△AOC∽△COB;
(3)求过A,B,C三点且对称轴平行于y轴的抛物线解析式;
(4)在抛物线上是否存在一点P(不与C重合),使得S
△ABP=S
△ABC?若存在,请求出P点坐标;若不存在,请说明理由.

查看答案和解析>>

 在平面直角坐标系内有两点A(-2,0),B(
在平面直角坐标系内有两点A(-2,0),B( ,0),CB所在直线为y=2x+b,
,0),CB所在直线为y=2x+b,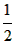 ,0),CB所在直线为y=2x+b。
,0),CB所在直线为y=2x+b。
 ,0),CB所在直线为y=2x+b,
,0),CB所在直线为y=2x+b,
 ,0),CB所在直线为y=2x+b,
,0),CB所在直线为y=2x+b,
 ,0),CB所在直线为y=2x+b,
,0),CB所在直线为y=2x+b,
 ,0),CB所在直线为y=2x+b,
,0),CB所在直线为y=2x+b,
 ,0),CB所在直线为y=2x+b,
,0),CB所在直线为y=2x+b,