
过(-1,0),(3,0),(1,2)三点的抛物线的顶点坐标是( )
|
科目:初中数学 来源:2011-2012学年浙江省绍兴市绍兴县成章中学九年级(上)第二次自我评价数学试卷(12月份)(解析版) 题型:选择题
 ,
,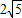 )点的反比例函数的图象应在 ( )
)点的反比例函数的图象应在 ( )科目:初中数学 来源:2010-2011学年浙江省温州市永嘉县黄田中学九年级(上)数学练习试卷(解析版) 题型:选择题
 ,
,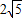 )点的反比例函数的图象应在 ( )
)点的反比例函数的图象应在 ( )科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:解答题
科目:初中数学 来源:不详 题型:填空题
科目:初中数学 来源:《1.3 线段的垂直平分线》2010年同步练习2(解析版) 题型:填空题
科目:初中数学 来源: 题型:
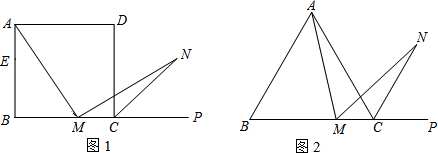
科目:初中数学 来源: 题型:



科目:初中数学 来源: 题型:
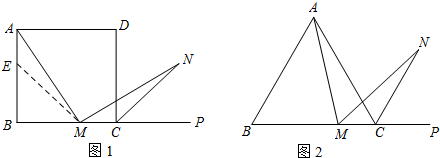 N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com