
在△ABC中,不能判定是等腰三角形的是( )
|
科目:初中数学 来源:不详 题型:单选题
| A.∠A:∠B:∠C=1:1:3 | B.a:b:c=2:2:3 |
| C.∠B=50°,∠C=80° | D.2∠A=∠B+∠C |
科目:初中数学 来源: 题型:单选题
科目:初中数学 来源: 题型:

科目:初中数学 来源: 题型:解答题
科目:初中数学 来源:不详 题型:解答题

科目:初中数学 来源: 题型:
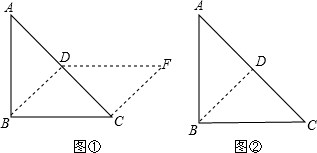
如图,把一个等腰直角三角形abc沿斜边上的高bd剪下,与剩下部分能拼成一个平行四边形bcfd(见示意图①)
(1)想一想——判断四边形bcfd是平行四边形的依据是
.(用平行四边形的判定方法叙述)
(2)做一做——按上述方法,请你拼一个与图①位置或形状不同的平行四边形,并在图
②中画出示意图.

图① 图②
科目:初中数学 来源: 题型:
如图,把一个等腰直角三角形ABC沿斜边上的高BD剪下,与剩下部分能拼成一个平行四边形BCFD(见示意图①)
(1)想一想——判断四边形BCFD是平行四边形的依据是
.(用平行四边形的判定方法叙述)
(2)做一做——按上述方法,请你拼一个与图①位置或形状不同的平行四边形,并在图
②中画出示意图.

图① 图②
科目:初中数学 来源: 题型:

| 1 | 2 |
科目:初中数学 来源: 题型:解答题
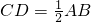 ,你能用矩形的性质说明这个结论吗?请说明.
,你能用矩形的性质说明这个结论吗?请说明.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com