
科目:初中数学 来源: 题型:
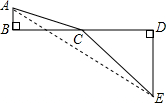 为了探索代数式
为了探索代数式| x2+1 |
| (8-x)2+25 |
| x2+1 |
| (8-x)2+25 |
| x2+1 |
| (8-x)2+25 |
| 4 |
| 3 |
| 4 |
| 3 |
| x2+4 |
| (12-x)2+9 |
科目:初中数学 来源: 题型:
 为了探索代数式
为了探索代数式| x2+1 |
| (8-x)2+25 |
| x2+1 |
| (8-x)2+25 |
| x2+1 |
| (8-x)2+25 |
| 4 |
| 3 |
| 4 |
| 3 |
| x2+4 |
| (12-x)2+9 |
科目:初中数学 来源:不详 题型:解答题
| x2+1 |
| (8-x)2+25 |
| x2+1 |
| (8-x)2+25 |
| x2+1 |
| (8-x)2+25 |
| x2+4 |
| (12-x)2+9 |

科目:初中数学 来源: 题型:解答题
 x+b,经过点M(0,
x+b,经过点M(0, ),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0),设x1=d(0<d<1).
),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0),设x1=d(0<d<1).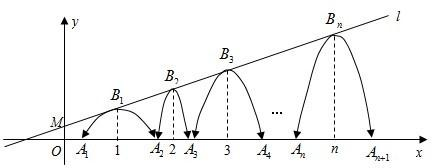
科目:初中数学 来源:广东省中考真题 题型:解答题
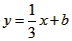 经过点
经过点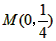 ,一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…,An+1(xn+1,0)(n为正整数),设x1=d(0<d<1)。
,一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…,Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1,0),A2(x2,0),A3(x3,0),…,An+1(xn+1,0)(n为正整数),设x1=d(0<d<1)。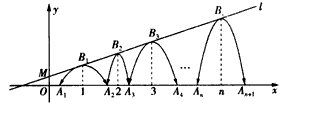
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com