
科目:高中数学 来源: 题型:
 A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲 |
| AB |
|
|
|
|
|
|
| n(2n-1) |
科目:高中数学 来源: 题型:
|
| α |
|
|
|
科目:高中数学 来源: 题型:
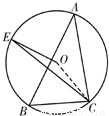
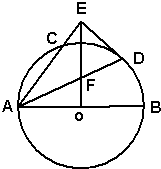 (1)如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于D,DE⊥AC交AC延长线于点E,OE交AD于点F.
(1)如图,AB是⊙O的直径,AC是弦,∠BAC的平分线AD交⊙O于D,DE⊥AC交AC延长线于点E,OE交AD于点F.| AC |
| AB |
| 3 |
| 5 |
| AF |
| DF |
|
科目:高中数学 来源:2010-2011学年江苏省南通市高三(上)期末数学试卷(解析版) 题型:解答题
 于点E,连接EC,求∠OEC.
于点E,连接EC,求∠OEC. ]的作用下变换为曲线C2,求C2的方程.
]的作用下变换为曲线C2,求C2的方程.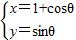 (θ为参数)上一点,求它到直线C2:
(θ为参数)上一点,求它到直线C2: (t为参数)距离的最小值.
(t为参数)距离的最小值.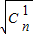 +
+ +L+
+L+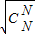 ≤
≤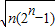 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com