
已知数列{an}的前n项和Sn=qn-1(q∈R,q≠0),则数列{an}( )
|
科目:高中数学 来源: 题型:
2 n |
科目:高中数学 来源:不详 题型:单选题
| A.一定是等差数列 |
| B.一定是等比数列 |
| C.或者是等差数列或等比数列 |
| D.既非等差数列又非等比数列 |
科目:高中数学 来源: 题型:单选题
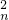 +1.
+1.科目:高中数学 来源: 题型:单选题
科目:高中数学 来源:模拟题 题型:解答题
 an(n∈N*),且a2=1。
an(n∈N*),且a2=1。科目:高中数学 来源: 题型:
科目:高中数学 来源: 题型:
 已知数列{an}的前n项和为Sn,a1=1,a4=8,Sn=b•qn+c(q≠0,q≠±1,bc≠0,b+c=0),现把数列{an}的各项排成如图所示的三角形形状.记A(m,n)为第m行从左起第n个数(m、n∈N*).有下列命题:
已知数列{an}的前n项和为Sn,a1=1,a4=8,Sn=b•qn+c(q≠0,q≠±1,bc≠0,b+c=0),现把数列{an}的各项排成如图所示的三角形形状.记A(m,n)为第m行从左起第n个数(m、n∈N*).有下列命题:| m-1 | 2m-1 |
科目:高中数学 来源: 题型:
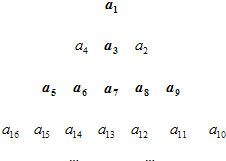 已知数列{an}的前n项和为Sn(n∈N*),a1=1,a4=8,Sn=b•qn-b(q≠0,q≠±1,b≠0),现把数列{an}的各项排成如图所示的三角形形状.记A(m,n)为第m行从左起第n个数.有下列命题:
已知数列{an}的前n项和为Sn(n∈N*),a1=1,a4=8,Sn=b•qn-b(q≠0,q≠±1,b≠0),现把数列{an}的各项排成如图所示的三角形形状.记A(m,n)为第m行从左起第n个数.有下列命题:科目:高中数学 来源: 题型:
| OPn |
| Sn |
| n |
| PmPn |
| b |
| 1 |
| 2 |
| OQn |
| an |
| n |
| Sn |
| n2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com