| 若f(x)=(m-2)x2+mx+(2m+1)=0的两个零点分别在区间(-1,0)和区间(1,2)内,则m的取值范围是( ) |
相关习题
科目:高中数学
来源:
题型:
若f(x)=(m-2)x2+mx+(2m+1)=0的两个零点分别在区间(-1,0)和区间(1,2)内,则m的取值范围是( )
查看答案和解析>>
科目:高中数学
来源:辽宁二模
题型:单选题
若f(x)=(m-2)x
2+mx+(2m+1)=0的两个零点分别在区间(-1,0)和区间(1,2)内,则m的取值范围是( )
查看答案和解析>>
科目:高中数学
来源:2009-2010学年北京市东城区高三(上)期末数学试卷(理科)(解析版)
题型:选择题
若f(x)=(m-2)x
2+mx+(2m+1)=0的两个零点分别在区间(-1,0)和区间(1,2)内,则m的取值范围是( )
A.(-

,

)
B.(-

,

)
C.(

,

)
D.[

,

]
查看答案和解析>>
科目:高中数学
来源:2013年辽宁省五校协作体高考数学二模试卷(理科)(解析版)
题型:选择题
若f(x)=(m-2)x
2+mx+(2m+1)=0的两个零点分别在区间(-1,0)和区间(1,2)内,则m的取值范围是( )
A.(-

,

)
B.(-

,

)
C.(

,

)
D.[

,

]
查看答案和解析>>
科目:高中数学
来源:2013年辽宁省五校协作体高考数学二模试卷(文科)(解析版)
题型:选择题
若f(x)=(m-2)x
2+mx+(2m+1)=0的两个零点分别在区间(-1,0)和区间(1,2)内,则m的取值范围是( )
A.(-

,

)
B.(-

,

)
C.(

,

)
D.[

,

]
查看答案和解析>>
科目:高中数学
来源:2010年宁夏高考等值诊断网上阅卷联考数学试卷(理科)(解析版)
题型:选择题
若f(x)=(m-2)x
2+mx+(2m+1)=0的两个零点分别在区间(-1,0)和区间(1,2)内,则m的取值范围是( )
A.(-

,

)
B.(-

,

)
C.(

,

)
D.[

,

]
查看答案和解析>>
科目:高中数学
来源:2011年高三数学单元检测:函数(1)(解析版)
题型:选择题
若f(x)=(m-2)x
2+mx+(2m+1)=0的两个零点分别在区间(-1,0)和区间(1,2)内,则m的取值范围是( )
A.(-

,

)
B.(-

,

)
C.(

,

)
D.[

,

]
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
若f(x)=(m-2)x2+mx+(2m+1)=0的两个零点分别在区间(-1,0)和区间(1,2)内,则m的取值范围是
- A.
(-

,

)
- B.
(-

,

)
- C.
(

,

)
- D.
[

,

]
查看答案和解析>>
科目:高中数学
来源:2011-2012学年浙江省金华市东阳中学高三(上)期中数学试卷(理科)(解析版)
题型:解答题
已知函数f(x)=-(2m+2)lnx+mx-

(m≥-1).
(I)讨论f(x)的单调性;
(II)设 g(x)=
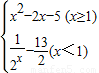
.当m=2时,若对任意x
1∈(0,2),存在x
2∈[k,k+1],(k∈N),使f(x
1)<g(x
2),求实数k的最小值.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知函数f(x)=4x
2-4mx+m
2-2m+2的图象与x轴有两个交点
(1)设两个交点的横坐标分别为x
1,x
2,试判断函数g(m)=x
12+x
22有没有最大值或最小值,并说明理由.
(2)若f(x)=4x
2-4mx+m
2-2m+2与g(x)=
在区间[2,3]上都是减函数,求实数m的取值范围.
查看答案和解析>>

 ,
, )
) ,
, )
) ,
, )
) ,
, ]
] ,
, )
) ,
, )
) ,
, )
) ,
, ]
] ,
, )
) ,
, )
) ,
, )
) ,
, ]
] ,
, )
) ,
, )
) ,
, )
) ,
, ]
] ,
, )
) ,
, )
) ,
, )
) ,
, ]
] ,
, )
) ,
, )
) ,
, )
) ,
, ]
] (m≥-1).
(m≥-1).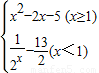 .当m=2时,若对任意x1∈(0,2),存在x2∈[k,k+1],(k∈N),使f(x1)<g(x2),求实数k的最小值.
.当m=2时,若对任意x1∈(0,2),存在x2∈[k,k+1],(k∈N),使f(x1)<g(x2),求实数k的最小值.