| 定义在R上的可导函数f(x)=x2+2xf′(2)+15,在闭区间[0,m]上有最大值15,最小值-1,则m的取值范围是( ) |
相关习题
科目:高中数学
来源:
题型:
定义在R上的可导函数f(x)=x2+2xf′(2)+15,在闭区间[0,m]上有最大值15,最小值-1,则m的取值范围是( )
查看答案和解析>>
科目:高中数学
来源:2011-2012学年浙江省杭州地区七校联考高三(上)期中数学试卷(理科)(解析版)
题型:选择题
定义在R上的可导函数f(x)=x2+2xf′(2)+15,在闭区间[0,m]上有最大值15,最小值-1,则m的取值范围是( )
A.m≥2
B.2≤m≤4
C.m≥4
D.4≤m≤8
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
定义在R上的可导函数f(x)=x
2+2xf′(2)+15,在闭区间[0,m]上有最大值15,最小值-1,则m的取值范围是( )
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
定义在R上的可导函数f(x)=x2+2xf′(2)+15,在闭区间[0,m]上有最大值15,最小值-1,则m的取值范围是
- A.
m≥2
- B.
2≤m≤4
- C.
m≥4
- D.
4≤m≤8
查看答案和解析>>
科目:高中数学
来源:
题型:
定义在R上的可导函数f(x)满足f(-x)=f(x),f(x-2)=f(x+2),且当x∈[2,4]时,f(x)=x
2+2xf
′(2),则f(-
)与f(
)的大小关系是( )
| A、f(-)=f() |
| B、f(-)<f() |
| C、f(-)>f() |
| D、不确定 |
查看答案和解析>>
科目:高中数学
来源:2012-2013学年浙江省杭州市建德市新安江中学高三(上)期中数学试卷(理科)(解析版)
题型:选择题
定义在R上的可导函数f(x)满足f(-x)=f(x),f(x-2)=f(x+2),且当x∈[2,4]时,f(x)=x
2+2xf
′(2),则f(-

)与f(
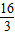
)的大小关系是( )
A.f(-

)=f(

)
B.f(-

)<f(
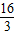
)
C.f(-

)>f(
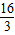
)
D.不确定
查看答案和解析>>
科目:高中数学
来源:2010-2011学年浙江省杭州市七校联考高三(上)期中数学试卷(理科)(解析版)
题型:选择题
定义在R上的可导函数f(x)满足f(-x)=f(x),f(x-2)=f(x+2),且当x∈[2,4]时,f(x)=x
2+2xf
′(2),则f(-

)与f(

)的大小关系是( )
A.f(-

)=f(

)
B.f(-

)<f(
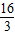
)
C.f(-

)>f(
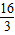
)
D.不确定
查看答案和解析>>
科目:高中数学
来源:2012-2013学年湖北省荆州中学高三第二次质量检测数学试卷(文科)(解析版)
题型:选择题
定义在R上的可导函数f(x)满足f(-x)=f(x),f(x-2)=f(x+2),且当x∈[2,4]时,f(x)=x
2+2xf
′(2),则f(-

)与f(
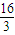
)的大小关系是( )
A.f(-

)=f(
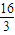
)
B.f(-

)<f(

)
C.f(-

)>f(

)
D.不确定
查看答案和解析>>
科目:高中数学
来源:2012-2013学年湖北省荆州中学高三第二次质量检测数学试卷(理科)(解析版)
题型:选择题
定义在R上的可导函数f(x)满足f(-x)=f(x),f(x-2)=f(x+2),且当x∈[2,4]时,f(x)=x
2+2xf
′(2),则f(-

)与f(

)的大小关系是( )
A.f(-

)=f(

)
B.f(-

)<f(

)
C.f(-

)>f(

)
D.不确定
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
定义在R上的可导函数f(x)满足f(-x)=f(x),f(x-2)=f(x+2),且当x∈[2,4]时,f(x)=x2+2xf′(2),则f(- )与f(
)与f(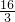 )的大小关系是
)的大小关系是
- A.
f(-

)=f(
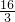
)
- B.
f(-

)<f(
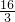
)
- C.
f(-

)>f(
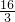
)
- D.
不确定
查看答案和解析>>

 )与f(
)与f(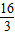 )的大小关系是( )
)的大小关系是( ) )=f(
)=f( )
) )<f(
)<f(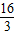 )
) )>f(
)>f(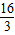 )
) )与f(
)与f( )的大小关系是( )
)的大小关系是( ) )=f(
)=f( )
) )<f(
)<f(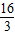 )
) )>f(
)>f(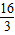 )
) )与f(
)与f(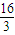 )的大小关系是( )
)的大小关系是( ) )=f(
)=f(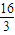 )
) )<f(
)<f( )
) )>f(
)>f( )
) )与f(
)与f( )的大小关系是( )
)的大小关系是( ) )=f(
)=f( )
) )<f(
)<f( )
) )>f(
)>f( )
) )与f(
)与f(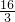 )的大小关系是
)的大小关系是 )=f(
)=f(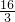 )
) )<f(
)<f(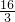 )
) )>f(
)>f(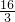 )
)