
A(-3,4)和B(4,-1)是平面直角坐标系中的两点,则由A点移到B点的路线可能是( )
|
科目:初中数学 来源: 题型:
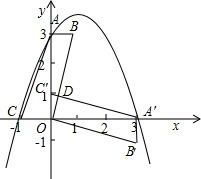 平面直角坐标系中,?ABOC如图放置,点A、C的坐标分别为(0,3)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到?A'B'OC'.
平面直角坐标系中,?ABOC如图放置,点A、C的坐标分别为(0,3)、(-1,0),将此平行四边形绕点O顺时针旋转90°,得到?A'B'OC'.科目:初中数学 来源: 题型:
| PD-PH |
| PM |
| PD-PH |
| PM |

科目:初中数学 来源: 题型:

科目:初中数学 来源:安徽省中考真题 题型:解答题
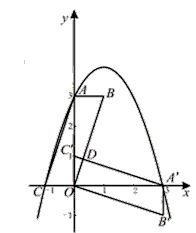
科目:初中数学 来源:安徽省中考真题 题型:解答题
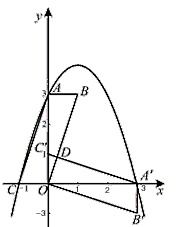
科目:初中数学 来源: 题型:
平面直角坐标系中,□ABOC如图放置,点A、C的坐标分别为(0,3)、(-1,0),将此平行四边形绕点O[顺时针旋转90°,得到□![]() .
.
(1)若抛物线过点![]() ,求此抛物线的解析式;
,求此抛物线的解析式;
(2)求□ABOC和□![]() 重叠部分
重叠部分![]() 的周长;
的周长;
(3)点M是![]() 第一象限内抛
第一象限内抛![]() 物线上的一动点,问:点M在何处时△
物线上的一动点,问:点M在何处时△![]() 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?
并求出此时点![]() 的坐标.
的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com