已知命题“?x∈R,x2+2ax+1<0”是真命题,则实数a的取值范围是( )| A.(-∞,-1) | B.(1,+∞) | C.(-∞,-1)∪(1,+∞) | D.(-1,1) |
|
相关习题
科目:高中数学
来源:
题型:
已知命题“?x∈R,x
2+2ax+1<0”是真命题,则实数a的取值范围是
(-∞,-1)∪(1,+∞)
(-∞,-1)∪(1,+∞)
.
查看答案和解析>>
科目:高中数学
来源:广东模拟
题型:单选题
已知命题“?x∈R,x
2+2ax+1<0”是真命题,则实数a的取值范围是( )
| A.(-∞,-1) | B.(1,+∞) | C.(-∞,-1)∪(1,+∞) | D.(-1,1) |
查看答案和解析>>
科目:高中数学
来源:2012-2013学年山东省临沂市临沭县高二(下)期中数学试卷(文科)(解析版)
题型:选择题
已知命题“?x∈R,x2+2ax+1<0”是真命题,则实数a的取值范围是( )
A.(-∞,-1)
B.(1,+∞)
C.(-∞,-1)∪(1,+∞)
D.(-1,1)
查看答案和解析>>
科目:高中数学
来源:2011-2012学年广东省深圳高级中学高三(上)第三次月考数学试卷(理科)(解析版)
题型:选择题
已知命题“?x∈R,x2+2ax+1<0”是真命题,则实数a的取值范围是( )
A.(-∞,-1)
B.(1,+∞)
C.(-∞,-1)∪(1,+∞)
D.(-1,1)
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
已知命题“?x∈R,x2+2ax+1<0”是真命题,则实数a的取值范围是
- A.
(-∞,-1)
- B.
(1,+∞)
- C.
(-∞,-1)∪(1,+∞)
- D.
(-1,1)
查看答案和解析>>
科目:高中数学
来源:广东省月考题
题型:单选题
已知命题“

x∈R,x
2+2ax+1<0”是真命题,则实数a的取值范围是
A.(﹣∞,﹣1)
B.(1,+∞)
C.(﹣∞,﹣1)∪(1,+∞)
D.(﹣1,1)
查看答案和解析>>
科目:高中数学
来源:广东省月考题
题型:单选题
已知命题“
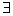
x∈R,x
2+2ax+1<0”是真命题,则实数a的取值范围是
A.(-∞,-1)
B.(1,+∞)
C.(-∞,-1)∪(1,+∞)
D.(-1,1)
查看答案和解析>>
科目:高中数学
来源:
题型:
(2011•广东模拟)已知命题“?x∈R,x2+2ax+1<0”是真命题,则实数a的取值范围是( )
查看答案和解析>>
科目:高中数学
来源:2012-2013学年江苏省连云港市新海高级中学高一(上)期中数学试卷(解析版)
题型:填空题
已知函数f(x)=|x2-2ax+a|(x∈R),给出下列四个命题:
①当且仅当a=0时,f(x)是偶函数;
②函数f(x)一定存在零点;
③函数在区间(-∞,a]上单调递减;
④当0<a<1时,函数f(x)的最小值为a-a2.
那么所有真命题的序号是 .
查看答案和解析>>
科目:高中数学
来源:2012-2013学年江苏省连云港市新海高级中学高一(上)期中数学试卷(解析版)
题型:填空题
已知函数f(x)=|x2-2ax+a|(x∈R),给出下列四个命题:
①当且仅当a=0时,f(x)是偶函数;
②函数f(x)一定存在零点;
③函数在区间(-∞,a]上单调递减;
④当0<a<1时,函数f(x)的最小值为a-a2.
那么所有真命题的序号是 .
查看答案和解析>>

 x∈R,x2+2ax+1<0”是真命题,则实数a的取值范围是
x∈R,x2+2ax+1<0”是真命题,则实数a的取值范围是 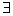 x∈R,x2+2ax+1<0”是真命题,则实数a的取值范围是
x∈R,x2+2ax+1<0”是真命题,则实数a的取值范围是