下列结论:①命题“?x∈R,x2-x>0”的否定是“?x∈R,x2-x≤0”;
②当x∈(1,+∞)时,函数y=x,y=x2的图象都在直线y=x的上方;
③定义在R上的奇函数f(x),满足f(x+2)=-f(x),则f(6)的值为0.
④若函数f(x)=mx2-2x在区间(2+∞)内是增函数,则实数m的取值范围为m ≥ .
其中,正确结论的个数是( ) |
相关习题
科目:高中数学
来源:
题型:
下列结论:①命题“?x∈R,x
2-x>0”的否定是“?x∈R,x
2-x≤0”;
②当x∈(1,+∞)时,函数
y=x,y=x2的图象都在直线y=x的上方;
③定义在R上的奇函数f(x),满足f(x+2)=-f(x),则f(6)的值为0.
④若函数f(x)=mx
2-2x在区间(2,+∞)内是增函数,则实数m的取值范围为
m ≥ .
其中,正确结论的个数是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
下列结论:①命题“?x∈R,x
2-x>0”的否定是“?x∈R,x
2-x≤0”;
②当x∈(1,+∞)时,函数
y=x,y=x2的图象都在直线y=x的上方;
③定义在R上的奇函数f(x),满足f(x+2)=-f(x),则f(6)的值为0.
④若函数f(x)=mx
2-2x在区间(2+∞)内是增函数,则实数m的取值范围为
m ≥ .
其中,正确结论的个数是( )
查看答案和解析>>
科目:高中数学
来源:
题型:
下列结论中正确命题的个数是
①命题p:“?x∈R,x
2-2≥0”的否定形式为?p:“?x∈R,x
2-2<0;
②若?p是q的必要条件,则p是?q的充分条件;
③“M>N”是“
()M>()N”的充分不必要条件( )
查看答案和解析>>
科目:高中数学
来源:济南一模
题型:单选题
下列结论中正确命题的个数是
①命题p:“?x∈R,x
2-2≥0”的否定形式为?p:“?x∈R,x
2-2<0;
②若?p是q的必要条件,则p是?q的充分条件;
③“M>N”是“
()M>()N”的充分不必要条件( )
查看答案和解析>>
科目:高中数学
来源:2012-2013学年福建省厦门六中高三(上)12月月考数学试卷(理科)(解析版)
题型:选择题
下列结论中正确命题的个数是
①命题p:“?x∈R,x
2-2≥0”的否定形式为¬p:“?x∈R,x
2-2<0;
②若¬p是q的必要条件,则p是¬q的充分条件;
③“M>N”是“
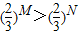
”的充分不必要条件( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学
来源:2011-2012学年江西省抚州市临川一中高三(上)第二次月考数学试卷(文科)(解析版)
题型:选择题
下列结论中正确命题的个数是
①命题p:“?x∈R,x
2-2≥0”的否定形式为¬p:“?x∈R,x
2-2<0;
②若¬p是q的必要条件,则p是¬q的充分条件;
③“M>N”是“

”的充分不必要条件( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学
来源:2011-2012学年陕西省榆林市府谷三中高三(上)第二次月考数学试卷(理科)(解析版)
题型:选择题
下列结论中正确命题的个数是
①命题p:“?x∈R,x
2-2≥0”的否定形式为¬p:“?x∈R,x
2-2<0;
②若¬p是q的必要条件,则p是¬q的充分条件;
③“M>N”是“
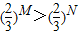
”的充分不必要条件( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学
来源:2011年宁夏固原一中高三适应性测试数学试卷3(文科)(解析版)
题型:选择题
下列结论中正确命题的个数是
①命题p:“?x∈R,x
2-2≥0”的否定形式为¬p:“?x∈R,x
2-2<0;
②若¬p是q的必要条件,则p是¬q的充分条件;
③“M>N”是“

”的充分不必要条件( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学
来源:2011年山东省济南市高考数学一模试卷(文科)(解析版)
题型:选择题
下列结论中正确命题的个数是
①命题p:“?x∈R,x
2-2≥0”的否定形式为¬p:“?x∈R,x
2-2<0;
②若¬p是q的必要条件,则p是¬q的充分条件;
③“M>N”是“

”的充分不必要条件( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学
来源:江西省月考题
题型:填空题
下列结论中正确命题的个数是
①命题p:“

x∈R,x
2﹣2≥0”的否定形式为

p:“

x∈R,x
2﹣2<0;
②若

p是q的必要条件,则p是

q的充分条件;
③“M>N”是“

”的充分不必要条件
A.0
B.1
C.2
D.3
查看答案和解析>>

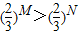 ”的充分不必要条件( )
”的充分不必要条件( ) ”的充分不必要条件( )
”的充分不必要条件( )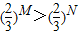 ”的充分不必要条件( )
”的充分不必要条件( ) ”的充分不必要条件( )
”的充分不必要条件( ) ”的充分不必要条件( )
”的充分不必要条件( ) x∈R,x2﹣2≥0”的否定形式为
x∈R,x2﹣2≥0”的否定形式为 p:“
p:“ x∈R,x2﹣2<0;
x∈R,x2﹣2<0; p是q的必要条件,则p是
p是q的必要条件,则p是 q的充分条件;
q的充分条件; ”的充分不必要条件
”的充分不必要条件