
设M={菱形},N={平行四边形},P={四边形},Q={正方形},则这些集合之间的关系为( )
|
科目:高中数学 来源:不详 题型:单选题
| A.P⊆N⊆M⊆Q | B.Q⊆M⊆N⊆P | C.P⊆M⊆N⊆Q | D.Q⊆N⊆M⊆P |
科目:高中数学 来源:2007-2008学年安徽省宣城市广德三中高一(上)第一次月考数学试卷(解析版) 题型:选择题
科目:高中数学 来源: 题型:单选题
科目:高中数学 来源: 题型:
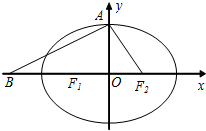 (2013•天津模拟)设椭圆C:
(2013•天津模拟)设椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| BF1 |
| F1F2 |
| 3 |
科目:高中数学 来源:2011年山东省临沂市高考数学一模试卷(文科)(解析版) 题型:解答题
 的左、右焦点分别为F1、F2,上顶点为A,△AF1F2为正三角形,且以AF2为直径的圆与直线
的左、右焦点分别为F1、F2,上顶点为A,△AF1F2为正三角形,且以AF2为直径的圆与直线 相切.
相切.科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
科目:高中数学 来源: 题型:解答题
 设椭圆C:
设椭圆C: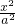 +
+ =1(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且2
=1(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且2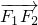 +
+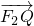 =
=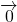 ,|F1F2|=2.
,|F1F2|=2.科目:高中数学 来源:2012-2013学年北京市十一学校高三(上)12月月考数学试卷(理科)(解析版) 题型:解答题
 +
+ =1(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且2
=1(a>b>0)的左、右焦点分别为F1,F2,上顶点为A,过点A与AF2垂直的直线交x轴负半轴于点Q,且2 +
+ =
= ,|F1F2|=2.
,|F1F2|=2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com