下面给出的四个不等式,其中正确的是( )| A.|2-i|>2i4 | B.|2+3i|>|1-4i| | C.3i>2i | D.i2>-i |
|
相关习题
科目:高中数学
来源:
题型:
下面给出的四个不等式,其中正确的是( )
| A、|2-i|>2i4 | B、|2+3i|>|1-4i| | C、3i>2i | D、i2>-i |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
下面给出的四个不等式,其中正确的是( )
| A.|2-i|>2i4 | B.|2+3i|>|1-4i| | C.3i>2i | D.i2>-i |
查看答案和解析>>
科目:高中数学
来源:2010-2011学年浙江省嘉兴市桐乡一中高二(上)第二次月考数学试卷(文理合卷)(解析版)
题型:选择题
下面给出的四个不等式,其中正确的是( )
A.|2-i|>2i4
B.|2+3i|>|1-4i|
C.3i>2i
D.i2>-i
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
下面给出的四个不等式,其中正确的是
- A.
|2-i|>2i4
- B.
|2+3i|>|1-4i|
- C.
3i>2i
- D.
i2>-i
查看答案和解析>>
科目:高中数学
来源:
题型:
给出下面四个不等式,其中正确的是( )
①sin1<cos1 ②sin2<cos2 ③sin190°>cos250°.
A.①② B.①③ C.① D.③
查看答案和解析>>
科目:高中数学
来源:2012年安徽省宿州市泗县一中高三数学考前最后一卷(文科)(解析版)
题型:解答题
给出以下结论:
①甲从四面体中任意选择一条棱,乙也从该四面体中任意选择一条棱,则所得的两条棱所在的直线是异面直线的概率是

;
②关于x的不等式

恒成立,则a的取值范围是

;
③若关于x的方程

上没有实数根,则k的取值范围是k≥2;
④函数f(x)=e
x-x-2(x≥0)有一个零点.
其中正确的结论是
(填上所有正确结论的序号)
查看答案和解析>>
科目:高中数学
来源:2011年安徽省合肥一中高考数学模拟最后一卷(文科)(解析版)
题型:解答题
给出以下结论:
①甲从四面体中任意选择一条棱,乙也从该四面体中任意选择一条棱,则所得的两条棱所在的直线是异面直线的概率是

;
②关于x的不等式

恒成立,则a的取值范围是

;
③若关于x的方程
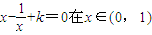
上没有实数根,则k的取值范围是k≥2;
④函数f(x)=e
x-x-2(x≥0)有一个零点.
其中正确的结论是
(填上所有正确结论的序号)
查看答案和解析>>
科目:高中数学
来源:
题型:
给出以下结论:
①甲从四面体中任意选择一条棱,乙也从该四面体中任意选择一条棱,则所得的两条棱所在的直线是异面直线的概率是
;
②关于x的不等式
a<sin2x+恒成立,则a的取值范围是
a<2;
③若关于x的方程
x-+k=0在x∈(0,1)上没有实数根,则k的取值范围是k≥2;
④函数f(x)=e
x-x-2(x≥0)有一个零点.
其中正确的结论是
①④
①④
(填上所有正确结论的序号)
查看答案和解析>>
科目:高中数学
来源:2010-2011学年安徽省六安一中高三(下)第七次月考数学试卷(理科)(解析版)
题型:填空题
给出下列四个命题:
①已知函数y=2sin(x+φ)(0<φ<π)的图象如图所示,则

;
②已知O、A、B、C是平面内不同的四点,且

,则α+β=1是A、B、C三点共线的充要条件;
③若数列a
n恒满足

(p为正常数,n∈N
*),则称数列a
n是“等方比数列”.根据此定义可以断定:若数列a
n是“等方比数列”,则它一定是等比数列;
④求解关于变量m、n的不定方程3n-2=2
m-1(n,m∈N
*),可以得到该方程中变量n的所有取值的表达式为

(k∈N
*).
其中正确命题的序号是
.

查看答案和解析>>

 ;
; 恒成立,则a的取值范围是
恒成立,则a的取值范围是 ;
; 上没有实数根,则k的取值范围是k≥2;
上没有实数根,则k的取值范围是k≥2; ;
; 恒成立,则a的取值范围是
恒成立,则a的取值范围是 ;
;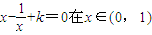 上没有实数根,则k的取值范围是k≥2;
上没有实数根,则k的取值范围是k≥2; ;
;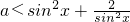 恒成立,则a的取值范围是
恒成立,则a的取值范围是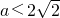 ;
;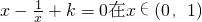 上没有实数根,则k的取值范围是k≥2;
上没有实数根,则k的取值范围是k≥2; ;
; ,则α+β=1是A、B、C三点共线的充要条件;
,则α+β=1是A、B、C三点共线的充要条件; (p为正常数,n∈N*),则称数列an是“等方比数列”.根据此定义可以断定:若数列an是“等方比数列”,则它一定是等比数列;
(p为正常数,n∈N*),则称数列an是“等方比数列”.根据此定义可以断定:若数列an是“等方比数列”,则它一定是等比数列;
