练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    函数y=sin(x+
    π
    2
    )，x∈R    （　　）
    A．是偶函数
    B．是奇函数
    C．既是偶函数又是奇函数
    D．既不是偶函数也不是奇函数
    A
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源：不详 题型：单选题

    函数y=sin(x+
    π
    2
    )，x∈R    （　　）
    A．是偶函数
    B．是奇函数
    C．既是偶函数又是奇函数
    D．既不是偶函数也不是奇函数

    查看答案和解析>>

    科目：高中数学 来源：2012年上海市浦东新区高考数学三模试卷（理科）（解析版） 题型：解答题

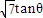    已知函数y=f（x），x∈D，y∈A；g（x）=x2-（4）x+1，
    （1）当f（x）=sin（x+φ）为偶函数时，求φ的值．
    （2）当f（x）=sin（2x+）+sin（2x+）时，g（x）在A上是单调递增函数，求θ的取值范围．
    （3）当f（x）=a1sin（ωx+φ1）+a2sin（ωx+φ2）+…+ansin（ωx+φn）时，（其中ai∈R，i=1，2，3…n，ω＞0），若f2（0）+f2（）≠0，且函数f（x）的图象关于点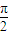（，0）对称，在x=π处取得最小值，试探讨ω应该满足的条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列说法：
    ①“?x∈R，2x＞3”的否定是“?x∈R，2x≤3”；
    ②命题“函数y=sin(?x+
    π
    3
    )    的最小正周期是π，则?=2”是真命题；
    ③命题“函数f（x）在x=x0处有极值，则f′（x0）=0”的否命题是假命题；
    ④f（x）是（-∞，0）∪（0，+∞）上的偶函数，x＞0时f（x）的解析式是f（x）=x3，
    则x＜0时f（x）的解析式是f（x）=-x3．
    其中正确的说法是（　　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    下列说法：
    ①“?x∈R，2x＞3”的否定是“?x∈R，2x≤3”；
    ②命题“函数y=sin(?x+
    π
    3
    )    的最小正周期是π，则?=2”是真命题；
    ③命题“函数f（x）在x=x0处有极值，则f′（x0）=0”的否命题是假命题；
    ④f（x）是（-∞，0）∪（0，+∞）上的偶函数，x＞0时f（x）的解析式是f（x）=x3，
    则x＜0时f（x）的解析式是f（x）=-x3．
    其中正确的说法是（　　）
    A．①③④B．①②③C．①②④D．②③④

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    定义在R上的函数y=sinx,y=sin2008,y=sin|x|,中，既是偶函数又是周期函数的个数是（　　）
    A．0个B．1个C．2个D．3个

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    定义在R上的偶函数y=f（x），满足f（x+1）=-f（x），且在[-3，-2]上是减函数，若α，β是锐角三角形的两个内角，则（　　）
    A．f（sinα）＞f（sinβ）B．f（cosα）＞f（cosβ）
    C．f（sinα）＜f（cosβ）D．f（sinα）＞f（cosβ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列命题中：
    ①若函数f（x）的定义域为R，则g（x）=f（x）+f（-x）一定是偶函数；
    ②直线x=
    π
    2
    是函数y=sin（2x-
    π
    2
    ）图象的一条对称轴；
    ③若1，a，b，c，4这五个数组成一个等比数列，则b=±2；
    ④若实数x，y满足
    x-y≤0
    x-2y+2≥0
    x≥-2
    ，则x+y的最大值是6；
    其中正确的命题序号是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年江西省南昌三中高三（上）10月月考数学试卷（理科）（解析版） 题型：选择题

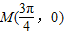    已知函数y=sin（ωx+φ）（ω＞0，0≤φ≤π）是R上的偶函数，其图象关于对称，且在区间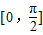上是单调函数，则满足条件的实数对（ω，φ）有（ ）
    A．1个
    B．2个
    C．3个
    D．4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列说法正确的是（　　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    下列说法正确的是（　　）
    A．存在α∈(0，
    π
    2
    ）使sinα+cosα=
    1
    3
    B．y=tanx在R内为增函数
    C．y=cos2x+sin（
    π
    2
    -x）是偶函数
    D．y=sin|2x+
    π
    6
    |最小正周期为π

    查看答案和解析>>


    同步练习册答案