| F1(-1,0),F2(1,0)是椭圆的两焦点,过F2的直线l交椭圆于P、Q两点,若△PF1Q的周长为16,则椭圆方程为( ) |
相关习题
科目:高中数学
来源:
题型:
已知F
1(-1,0),F
2(1,0)是椭圆C的两个焦点,A、B为过F
1的直线与椭圆的交点,且△F
2AB的周长为
4.
(Ⅰ)求椭圆C的方程;
(Ⅱ)判断
+是否为定值,若是求出这个值,若不是说明理由.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知F1(-1,0),F2(1,0)是椭圆C的两个焦点,过F2且垂直于x轴的直线交于A、B两点,且|AB|=3,则C的方程为( )
查看答案和解析>>
科目:高中数学
来源:
题型:
F1(-1,0)、F2(1,0)是椭圆的两焦点,过F1的直线l交椭圆于M、N,若△MF2N的周长为8,则椭圆方程为( )
查看答案和解析>>
科目:高中数学
来源:
题型:
已知F
1(-1,0),F
2(1,0)是椭圆
+
=1的两个焦点,点G与F
2关于直线l:x-2y+4=0对称,且GF
1与l的交点P在椭圆上.
(I)求椭圆方程;
(II)若P、M(x
1,y
1),N(x
2,y
2)是椭圆上的不同三点,直线PM、PN的倾斜角互补,问直线MN的斜率是否是定值?如果是,求出该定值,如果不是,说明理由.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
F
1(-1,0)、F
2(1,0)是椭圆的两焦点,过F
1的直线l交椭圆于M、N,若△MF
2N的周长为8,则椭圆方程为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知F
1(-1,0),F
2(1,0)是椭圆C的两个焦点,过F
2且垂直于x轴的直线交于A、B两点,且|AB|=3,则C的方程为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知F
1(-1,0),F
2(1,0)是椭圆
+
=1的两个焦点,点G与F
2关于直线l:x-2y+4=0对称,且GF
1与l的交点P在椭圆上.
(I)求椭圆方程;
(II)若P、M(x
1,y
1),N(x
2,y
2)是椭圆上的不同三点,直线PM、PN的倾斜角互补,问直线MN的斜率是否是定值?如果是,求出该定值,如果不是,说明理由.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年湖北省襄阳市宜城三中高二(下)期中数学试卷(文科)(解析版)
题型:选择题
F
1(-1,0)、F
2(1,0)是椭圆的两焦点,过F
1的直线l交椭圆于M、N,若△MF
2N的周长为8,则椭圆方程为( )
A.

B.

C.

D.

查看答案和解析>>
科目:高中数学
来源:2007年广东省汕头市潮阳一中高三摸底数学试卷(文科)(解析版)
题型:选择题
F
1(-1,0)、F
2(1,0)是椭圆的两焦点,过F
1的直线l交椭圆于M、N,若△MF
2N的周长为8,则椭圆方程为( )
A.

B.

C.

D.

查看答案和解析>>
科目:高中数学
来源:2010年甘肃省天水一中高考数学三模试卷(理科)(解析版)
题型:解答题
已知F
1(-1,0),F
2(1,0)是椭圆
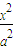
+
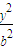
=1的两个焦点,点G与F
2关于直线l:x-2y+4=0对称,且GF
1与l的交点P在椭圆上.
(I)求椭圆方程;
(II)若P、M(x
1,y
1),N(x
2,y
2)是椭圆上的不同三点,直线PM、PN的倾斜角互补,问直线MN的斜率是否是定值?如果是,求出该定值,如果不是,说明理由.
查看答案和解析>>









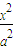 +
+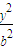 =1的两个焦点,点G与F2关于直线l:x-2y+4=0对称,且GF1与l的交点P在椭圆上.
=1的两个焦点,点G与F2关于直线l:x-2y+4=0对称,且GF1与l的交点P在椭圆上.