已知函数f(x)对任意实数x均有f(-x)=-f(x),f(π-x)=f(x)成立,当x∈[0,]时,f(x)=cosx-1.则当x∈[π,2π]时,函数f(x)的表达式为( )| A.cosx+1 | B.cosx-1 | C.-cosx-1 | D.-cosx+1 |
|
相关习题
科目:高中数学
来源:
题型:
已知函数f(x)对任意实数x均有f(x)=kf(x+2),其中常数k为负数,且f(x)在区间[0,2]上有表达式f(x)=x(x-2).
(1)求f(-1),f(2.5)的值;
(2)写出f(x)在[-3,3]上的表达式,并讨论函数f(x)在[-3,3]上的单调性;
(3)求出f(x)在[-3,3]上的最小值和最大值,并求出相应的自变量的取值.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知函数f(x)对任意实数x均有f(x)=2f(x+2),且f(x)在区间[0,2]上有表达式f(x)=x(x-2).
(Ⅰ)求f(-1),f(2.5)的值;
(Ⅱ)写出f(x)在[-3,3]上的表达式.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知函数f(x)对任意实数x均有f(x)=kf(x+2),常数k<0,且k<0,且f(x)在区间[0,2]上有表达式f(x)=x(x-2)
(1)求f(-1),f(2.5);
(2)若k=-2,写出f(x)在[-3,3]上得表达式,并讨论函数f(x)在[-3,3]上得单调性;
(3)求f(x)在[-3,3]上得最小值和最大值,并求出相应的自变量的取值.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知函数f(x)对任意实数x均有f(x)=kf(x+2),其中常数k<0,且f(x)在区间[0,2]的表达式为f(x)=x(x-2).
(1)求f(-1),f(2.5)的值(用k表示);
(2)写出f(x)在区间[-3,2]上的表达式,并讨论f(x)在[-3,2]上的单调性(不要求证明);
(3)求出f(x)在区间[-3,2]上的最小值与最大值,并求出相应的自变量的取值.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知函数f(x)对任意实数x均有f(-x)=-f(x),f(π-x)=f(x)成立,当
x∈[0,]时,f(x)=cosx-1.则当
x∈[π,2π]时,函数f(x)的表达式为( )
查看答案和解析>>
科目:高中数学
来源:
题型:
已知函数f(x)对任意实数x均有f(x)=-f(x+2),且f(x)在区间[0,2]上有表达式f(x)=x(x-2).
(1)求f(-1),f(2.5)的值;
(2)写出f(x)在[-3,3]上的表达式,设g(x)=f(x)-k(k∈R),随着k的变化讨论函数g(x)在区间[-3,3]上零点的个数
(3)体会(2)中解析式的求法,试求出f(x)在R上的解析式,给出函数的单调区间;并求出x为何值时,f(x)有最大值.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年北京市东城区(南片)高二(下)期末数学试卷(文科)(解析版)
题型:解答题
已知函数f(x)对任意实数x均有f(x)=2f(x+2),且f(x)在区间[0,2]上有表达式f(x)=x(x-2).
(Ⅰ)求f(-1),f(2.5)的值;
(Ⅱ)写出f(x)在[-3,3]上的表达式.
查看答案和解析>>
科目:高中数学
来源:2011-2012学年江苏省苏州一中学高一(上)期中数学试卷(解析版)
题型:解答题
已知函数f(x)对任意实数x均有f(x)=kf(x+2),常数k<0,且k<0,且f(x)在区间[0,2]上有表达式f(x)=x(x-2)
(1)求f(-1),f(2.5);
(2)若k=-2,写出f(x)在[-3,3]上得表达式,并讨论函数f(x)在[-3,3]上得单调性;
(3)求f(x)在[-3,3]上得最小值和最大值,并求出相应的自变量的取值.
查看答案和解析>>
科目:高中数学
来源:2008-2009学年湖北省武汉二中高一(下)期末数学试卷(理科)(解析版)
题型:选择题
已知函数f(x)对任意实数x均有f(-x)=-f(x),f(π-x)=f(x)成立,当

时,f(x)=cosx-1.则当

时,函数f(x)的表达式为( )
A.cosx+1
B.cosx-1
C.-cosx-1
D.-cosx+1
查看答案和解析>>
科目:高中数学
来源:2008-2009学年湖北省武汉二中高一(下)期末数学试卷(文科)(解析版)
题型:选择题
已知函数f(x)对任意实数x均有f(-x)=-f(x),f(π-x)=f(x)成立,当
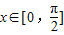
时,f(x)=cosx-1.则当

时,函数f(x)的表达式为( )
A.cosx+1
B.cosx-1
C.-cosx-1
D.-cosx+1
查看答案和解析>>

 时,f(x)=cosx-1.则当
时,f(x)=cosx-1.则当 时,函数f(x)的表达式为( )
时,函数f(x)的表达式为( )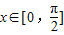 时,f(x)=cosx-1.则当
时,f(x)=cosx-1.则当 时,函数f(x)的表达式为( )
时,函数f(x)的表达式为( )