| 设首项不为零的等差数列{an}前n项之和是Sn,若不等式an2+≥λa12对任意{an}和正整数n恒成立,则实数λ的最大值为( ) |
相关习题
科目:高中数学
来源:
题型:
设首项不为零的等差数列{a
n}前n项之和是S
n,若不等式
an2+≥λa12对任意{a
n}和正整数n恒成立,则实数λ的最大值为( )
查看答案和解析>>
科目:高中数学
来源:
题型:
设首项不为零的等差数列{a
n}前n项之和是S
n,若不等式
an2+≥λa12对任意a
n和正整数n恒成立,则实数λ的最大值为
.
查看答案和解析>>
科目:高中数学
来源:宜春一模
题型:单选题
设首项不为零的等差数列{a
n}前n项之和是S
n,若不等式
an2+≥λa12对任意{a
n}和正整数n恒成立,则实数λ的最大值为( )
查看答案和解析>>
科目:高中数学
来源:2010-2011学年湖北省孝感市英才高中高一(下)第一次月考数学试卷(文科)(解析版)
题型:选择题
设首项不为零的等差数列{a
n}前n项之和是S
n,若不等式

对任意{a
n}和正整数n恒成立,则实数λ的最大值为( )
A.0
B.

C.

D.1
查看答案和解析>>
科目:高中数学
来源:2010-2011学年湖南省株洲二中高三(上)第三次月考数学试卷(理科)(解析版)
题型:选择题
设首项不为零的等差数列{a
n}前n项之和是S
n,若不等式

对任意{a
n}和正整数n恒成立,则实数λ的最大值为( )
A.0
B.

C.

D.1
查看答案和解析>>
科目:高中数学
来源:2012年江苏省四星高中高三数学小题训练(5)(解析版)
题型:解答题
设首项不为零的等差数列{a
n}前n项之和是S
n,若不等式

对任意a
n和正整数n恒成立,则实数λ的最大值为
.
查看答案和解析>>
科目:高中数学
来源:2010年江苏省南通中学高三数学最后10天冲刺试卷(2)(解析版)
题型:解答题
设首项不为零的等差数列{a
n}前n项之和是S
n,若不等式

对任意a
n和正整数n恒成立,则实数λ的最大值为
.
查看答案和解析>>
科目:高中数学
来源:2011年重庆十一中高考数学一模训练试卷(二)(解析版)
题型:解答题
设首项不为零的等差数列{a
n}前n项之和是S
n,若不等式
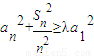
对任意a
n和正整数n恒成立,则实数λ的最大值为
.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知等差数列{a
n}的首项a
1=1,公差d>0,且第二项、第五项、第十四项分别是等比数列{b
n}的第二项、第三项、第四项.
(I)求数列{a
n}与{b
n}的通项公式;
(Ⅱ)设数列{c
n}对任意正整数n均有
+
+
+…+
=(n+1)a
n+1成立,其中m为不等于零的常数,求数列{c
n}的前n项和S
n.
查看答案和解析>>
科目:高中数学
来源:
题型:
设数列{a
n}的前n项和为S
n,如果
为常数,则称数列{a
n}为“科比数列”.
(Ⅰ)已知等差数列{b
n}的首项为1,公差不为零,若{b
n}为“科比数列”,求{b
n}的通项公式;
(Ⅱ)设数列{c
n}的各项都是正数,前n项和为S
n,若c
13+c
23+c
33+…+c
n3=S
n2对任意n∈N
*都成立,试推断数列{c
n}是否为“科比数列”?并说明理由.
查看答案和解析>>

 对任意{an}和正整数n恒成立,则实数λ的最大值为( )
对任意{an}和正整数n恒成立,则实数λ的最大值为( )

 对任意{an}和正整数n恒成立,则实数λ的最大值为( )
对任意{an}和正整数n恒成立,则实数λ的最大值为( )

 对任意an和正整数n恒成立,则实数λ的最大值为 .
对任意an和正整数n恒成立,则实数λ的最大值为 . 对任意an和正整数n恒成立,则实数λ的最大值为 .
对任意an和正整数n恒成立,则实数λ的最大值为 .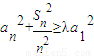 对任意an和正整数n恒成立,则实数λ的最大值为 .
对任意an和正整数n恒成立,则实数λ的最大值为 .