
a,b,c∈(0,+∞)且表示线段长度,则a,b,c能构成锐角三角形的充要条件是( )
|
科目:高中数学 来源:不详 题型:单选题
| A.a2+b2<c2 | B.|a2-b2|<c2 |
| C.|a-b|<c<|a+b| | D.|a2-b2|<c2<a2+b2 |
科目:高中数学 来源:2010年广东省广州市越秀区高考数学一轮双基小题练习(10)(解析版) 题型:选择题
科目:高中数学 来源:2010年新教材高考数学模拟题详解精编试卷(4)(解析版) 题型:选择题
科目:高中数学 来源: 题型:单选题
科目:高中数学 来源: 题型:
(本小题满分14分)已知动圆过定点F(2,0),且与直线![]() 相切。(1)求动圆圆心的轨迹C的方程;(2)若经过定点F的动直线
相切。(1)求动圆圆心的轨迹C的方程;(2)若经过定点F的动直线![]() 与轨迹C交于A、B两点,且这两点的横坐标分别为
与轨迹C交于A、B两点,且这两点的横坐标分别为![]() .①求证:
.①求证:![]() 为定值;②试用
为定值;②试用![]() 表示线段AB的长度;③求线段AB长度的最小值。
表示线段AB的长度;③求线段AB长度的最小值。
科目:高中数学 来源:不详 题型:解答题
 相切。(1)求动圆圆心的轨迹C的方程;(2)若经过定点F的动直线
相切。(1)求动圆圆心的轨迹C的方程;(2)若经过定点F的动直线 与轨迹C交于A、B两点,且这两点的横坐标分别为
与轨迹C交于A、B两点,且这两点的横坐标分别为 .①求证:
.①求证: 为定值;②试用
为定值;②试用 表示线段AB的长度;③求线段AB长度的最小值。
表示线段AB的长度;③求线段AB长度的最小值。科目:高中数学 来源:0103 期中题 题型:解答题
 长轴长与短轴长之差是2
长轴长与短轴长之差是2 -2,且右焦点F到此椭圆一个短轴端点的距离为
-2,且右焦点F到此椭圆一个短轴端点的距离为 ,点C(m,0)是线段OF上的一个动点(O为坐标原点)。
,点C(m,0)是线段OF上的一个动点(O为坐标原点)。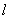 与椭圆交于A、B两点,使得
与椭圆交于A、B两点,使得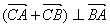 ,并说明理由。
,并说明理由。 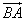 的方向向量可表示为(1,k)】
的方向向量可表示为(1,k)】 科目:高中数学 来源:2013年高考数学复习卷C(六)(解析版) 题型:解答题
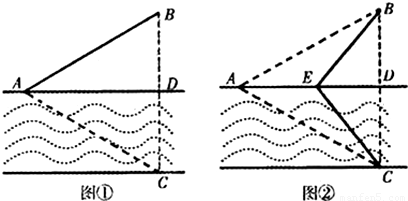
 ),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.
),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.科目:高中数学 来源:2012年福建省福州市高三3月质量检查数学试卷(理科)(解析版) 题型:解答题

 ),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.
),试用θ表示出总施工费用y(万元)的解析式,并求y的最小值.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com