
现有甲、乙两骰子,从1点到6点出现的概率都是1/6,掷甲、乙两颗骰子,设分别出现的点数为a、b时,则满足a<|b2-2a|<
|
科目:高中数学 来源:2010年广东省高考冲刺强化训练试卷六文科数学 题型:选择题
现有甲、乙两骰子,从1点到6点出现的概率都是1/6,掷甲、乙两颗骰子,设分别出现的点数为a、b时,则满足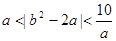 的概率为( )
的概率为( )
A、 B、
B、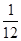 C、
C、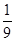 D、
D、
科目:高中数学 来源:不详 题型:单选题
| 10 |
| a |
A.
| B.
| C.
| D.
|
科目:高中数学 来源:2011年辽宁省沈阳二中高考数学五模试卷(文科)(解析版) 题型:选择题
 的概率为( )
的概率为( )
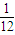


科目:高中数学 来源:2010年广东省高考数学冲刺预测试卷06(理科)(解析版) 题型:选择题
 的概率为( )
的概率为( )



科目:高中数学 来源: 题型:
| 1 |
| 6 |
| 10 |
| a |
A、
| ||
B、
| ||
C、
| ||
D、
|
科目:高中数学 来源:2014届甘肃天水一中高二下学期期末考试文科数学试卷(解析版) 题型:解答题
天水市第一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,
规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,
得到如下的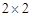 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为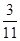 .
.
|
|
优秀 |
非优秀 |
合计 |
|
甲班 |
10 |
|
|
|
乙班 |
|
30 |
|
|
合计 |
|
|
110 |
(1)请完成上面的列联表;
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号。试求抽到9号或10号的概率。
参考公式与临界值表: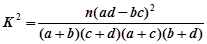 。
。
|
|
0.100 |
0.050 |
0.025 |
0.010 |
0.001 |
|
|
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
科目:高中数学 来源: 题型:
| 3 |
| 11 |
| 优秀 | 非优秀 | 合计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 110 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com