
| 若平面直角坐标系中两点M,N满足条件: ①M,N分别在函数f(x),g(x)的图象上; ②M,N关于(1,O)对称,则称点对(M,N)是一个“相望点对”(说明:(M,N)和(N,M)是同一个“相望点对”). 函数y=
|
科目:高中数学 来源:许昌三模 题型:单选题
| 1 |
| 1-x |
| A.2 | B.4 | C.6 | D.8 |
科目:高中数学 来源: 题型:
| OC |
| OM |
| ON |
| OA |
| OB |
科目:高中数学 来源: 题型:
| OC |
| OM |
| ON |
| OA |
| OB |
科目:高中数学 来源: 题型:
| OC |
| OA |
| OB |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| a2 |
| 1 |
| b2 |
| ||
| 2 |
科目:高中数学 来源: 题型:
| 1 |
| 1-x |
科目:高中数学 来源: 题型:
(12分)平面直角坐标系中,O为坐标原点,给定两点A(1,0)、B(0,-2),点C满足![]() 、
、![]() .
.
(Ⅰ)求点C的轨迹方程;
(Ⅱ)设点C的轨迹与双曲线![]() 交于两点M、N,且以MN为直径的圆过原点,求证
交于两点M、N,且以MN为直径的圆过原点,求证![]() ;
;
(Ⅲ)在(Ⅱ)的条件下,若双曲线的离心率不大于![]() ,求双曲线实轴长的取值范围.
,求双曲线实轴长的取值范围.
科目:高中数学 来源: 题型:
科目:高中数学 来源: 题型:
科目:高中数学 来源:2008-2009学年重庆市西南师大附中高三(上)2月月考数学试卷(文科)(解析版) 题型:解答题
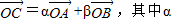 、β∈R,且α-2β=1
、β∈R,且α-2β=1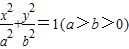 交于两点M、N,且以MN为直径的圆过原点,求证:
交于两点M、N,且以MN为直径的圆过原点,求证: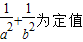 ;
;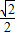 ,求椭圆长轴长的取值范围.
,求椭圆长轴长的取值范围.科目:高中数学 来源:2007-2008学年江苏省南通市启东中学高三(上)期末数学复习试卷1(解析版) 题型:解答题
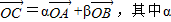 、β∈R,且α-2β=1
、β∈R,且α-2β=1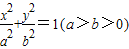 交于两点M、N,且以MN为直径的圆过原点,求证:
交于两点M、N,且以MN为直径的圆过原点,求证: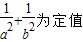 ;
; ,求椭圆长轴长的取值范围.
,求椭圆长轴长的取值范围.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com