| 已知三条直线l1:4x+y=1,l2:x-y=0,l3:2x-my=3,若l1关于l2的对称直线与l3垂直,则实数m的值是( ) |
相关习题
科目:高中数学
来源:
题型:
已知三条直线l1:4x+y=1,l2:x-y=0,l3:2x-my=3,若l1关于l2的对称直线与l3垂直,则实数m的值是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知三条直线l
1:4x+y=1,l
2:x-y=0,l
3:2x-my=3,若l
1关于l
2的对称直线与l
3垂直,则实数m的值是( )
查看答案和解析>>
科目:高中数学
来源:2010-2011学年安徽省巢湖市高三(上)质量检测数学试卷(理科)(解析版)
题型:选择题
已知三条直线l
1:4x+y=1,l
2:x-y=0,l
3:2x-my=3,若l
1关于l
2的对称直线与l
3垂直,则实数m的值是( )
A.-8
B.

C.8
D.

查看答案和解析>>
科目:高中数学
来源:
题型:单选题
已知三条直线l1:4x+y=1,l2:x-y=0,l3:2x-my=3,若l1关于l2的对称直线与l3垂直,则实数m的值是
- A.
-8
- B.
- C.
8
- D.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知三条直线l
1:2x-y+a=0(a>0),直线l
2:-4x+2y+1=0和直线l
3:x+y-1=0,且l
1与l
2的距离是
.
(1)求a的值;
(2)求l
3到l
1的角θ;
(3)能否找到一点P,使得P点同时满足下列三个条件:①P是第一象限的点;②P点到l
1的距离是P点到l
2的距离的
;③P点到l
1的距离与P点到l
3的距离之比是
:
?若能,求P点坐标;若不能,请说明理由.
查看答案和解析>>
科目:高中数学
来源:
题型:
已知三条直线l
1:2x-y+a=0(a>0),l
2:-4x+2y+1=0和l
3:x+y-1=0,且l
1与l
2的距离是
;
(1)求a的值;
(2)能否找到一点P同时满足下列三个条件:
①P是第一象限的点;
②点P到l
1的距离是点P到l
2的距离的
;
③点P到l
1的距离与点P到l
3的距离之比是
:
?若能,求点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:高中数学
来源:2012-2013学年江苏省泰州市泰兴市高一(下)期末数学试卷(解析版)
题型:解答题
已知三条直线l
1:2x-y+a=0(a>0),直线l
2:-4x+2y+1=0和直线l
3:x+y-1=0,且l
1与l
2的距离是


.
(1)求a的值;
(2)求l
3到l
1的角θ;
(3)能否找到一点P,使得P点同时满足下列三个条件:①P是第一象限的点;②P点到l
1的距离是P点到l
2的距离的

;③P点到l
1的距离与P点到l
3的距离之比是

:

?若能,求P点坐标;若不能,请说明理由.
查看答案和解析>>
科目:高中数学
来源:2006年高考第一轮复习数学:7.2 两直线的位置关系(解析版)
题型:解答题
已知三条直线l
1:2x-y+a=0(a>0),直线l
2:-4x+2y+1=0和直线l
3:x+y-1=0,且l
1与l
2的距离是


.
(1)求a的值;
(2)求l
3到l
1的角θ;
(3)能否找到一点P,使得P点同时满足下列三个条件:①P是第一象限的点;②P点到l
1的距离是P点到l
2的距离的

;③P点到l
1的距离与P点到l
3的距离之比是

:

?若能,求P点坐标;若不能,请说明理由.
查看答案和解析>>
科目:高中数学
来源:广东省高考数学一轮复习:8.4 两条直线的交点、距离(解析版)
题型:解答题
已知三条直线l
1:2x-y+a=0(a>0),直线l
2:-4x+2y+1=0和直线l
3:x+y-1=0,且l
1与l
2的距离是


.
(1)求a的值;
(2)求l
3到l
1的角θ;
(3)能否找到一点P,使得P点同时满足下列三个条件:①P是第一象限的点;②P点到l
1的距离是P点到l
2的距离的

;③P点到l
1的距离与P点到l
3的距离之比是

:

?若能,求P点坐标;若不能,请说明理由.
查看答案和解析>>





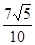 .
. ;
;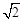 ∶
∶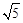 .若能,求P点坐标;若不能,说明理由.
.若能,求P点坐标;若不能,说明理由.
 .
. ;③P点到l1的距离与P点到l3的距离之比是
;③P点到l1的距离与P点到l3的距离之比是 :
: ?若能,求P点坐标;若不能,请说明理由.
?若能,求P点坐标;若不能,请说明理由.
 .
. ;③P点到l1的距离与P点到l3的距离之比是
;③P点到l1的距离与P点到l3的距离之比是 :
: ?若能,求P点坐标;若不能,请说明理由.
?若能,求P点坐标;若不能,请说明理由.
 .
. ;③P点到l1的距离与P点到l3的距离之比是
;③P点到l1的距离与P点到l3的距离之比是 :
: ?若能,求P点坐标;若不能,请说明理由.
?若能,求P点坐标;若不能,请说明理由.