
 到达途中的C市;慢车于下午4点到达C市.那么两车相遇时刻是________;慢车到达A市的时刻是________.
到达途中的C市;慢车于下午4点到达C市.那么两车相遇时刻是________;慢车到达A市的时刻是________. ,因为两者的速度比为4:3,所以慢车9点时驶了全程的(
,因为两者的速度比为4:3,所以慢车9点时驶了全程的(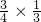 );9点后慢车继续行驶于下午4点到达C市,用的时间为(12+4-9),那么慢车的速度应为(1-
);9点后慢车继续行驶于下午4点到达C市,用的时间为(12+4-9),那么慢车的速度应为(1- -
-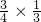 )÷(12+4-9),求出慢车的速度相应的就能求出快车的速度,求出两车速度之后,相遇时间,慢车到达A市的时间就容易求出了.
)÷(12+4-9),求出慢车的速度相应的就能求出快车的速度,求出两车速度之后,相遇时间,慢车到达A市的时间就容易求出了. -
-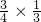 )÷(12+4-9)=
)÷(12+4-9)= ÷7=
÷7=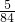 ,
,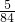 ÷
÷ =
=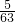 ,
, -
-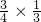 )÷(
)÷(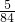 +
+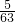 )=9+
)=9+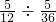 =9+3=12 (时),
=9+3=12 (时), ÷
÷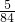 =5.6(时)=5(时)36(分),
=5.6(时)=5(时)36(分),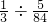 =21.6(时)=21(时)36(分),
=21.6(时)=21(时)36(分),

 全优点练单元计划系列答案
全优点练单元计划系列答案科目:小学数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com