


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:小学数学 来源: 题型:
查看答案和解析>>
科目:小学数学 来源: 题型:
查看答案和解析>>
科目:小学数学 来源: 题型:
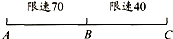 如图,A与B、B与C之间的公路长度相等,且每段公路上都有限速标志(单位:千米/时).甲货车从A出发,乙货车从C出发,并且两车在A、C之间往返行驶.结果当甲车到达C后再返回到B时,乙车刚好第一次到达B.已知甲、乙两车在各段公路上均以所能达到的最快速度行驶(不会超过车子本身的最高时速,也不能超过公路上的最高限速),且甲车的最高时速是乙车的4倍,那么甲车的最高时速是多少?
如图,A与B、B与C之间的公路长度相等,且每段公路上都有限速标志(单位:千米/时).甲货车从A出发,乙货车从C出发,并且两车在A、C之间往返行驶.结果当甲车到达C后再返回到B时,乙车刚好第一次到达B.已知甲、乙两车在各段公路上均以所能达到的最快速度行驶(不会超过车子本身的最高时速,也不能超过公路上的最高限速),且甲车的最高时速是乙车的4倍,那么甲车的最高时速是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com