Question

4．如图，已知正方形ABCD的周长是40厘米，DE=6.4厘米，阴影部分的面积是32平方厘米．

Answer 1

分析 如下图所示：连接BD，由等底等高的三角形的面积相等，可知三角形BCD的面积等于三角形BCF的面积，依据等式的性质，把它们的面积都减去重合部分的三角形BCE的面积，剩下的面积也相等，即三角形BDE的面积等于三角形CEF即阴影部分的面积．由此可知，求阴影部分的面积也就是求三角形BDE的面积，已知正方形的周长，用周长除以4即可得到正方形的边长，即三角形BDE的底边DE上的高，再利用三角形的面积公式代入数据即可解决．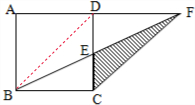

解答 解：由分析可知阴影部分的面积为：
6.4×（40÷4）÷2
=6.4×10÷2
=64÷2
=32（平方厘米）；
答：阴影部分的面积是32平方厘米．
故答案为：32．

点评 本题解决的关键是利用转化的数学思想方法，把求阴影部分的面积转化为易求面积的三角形的面积，从而利用三角形的面积公式解决问题．