
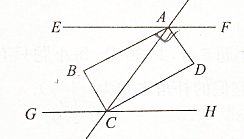
 如图,已知EF∥GH,又AB,AD,CB,CD分别是∠EAC,∠FAC,∠GCA,∠HCA的平分线,若AC与EF不垂直,则图中与∠BAD相等的角是∠BCD.
如图,已知EF∥GH,又AB,AD,CB,CD分别是∠EAC,∠FAC,∠GCA,∠HCA的平分线,若AC与EF不垂直,则图中与∠BAD相等的角是∠BCD. 分析 如下图所示,因为EF∥GH,由平行线的性质可知,∠EAC=∠HCA,∠FAC=∠GCA,又因为AB,AD,CB,CD分别是∠EAC,∠FAC,∠GCA,∠HCA的平分线,所以∠1=$\frac{1}{2}$∠EAC,∠2=$\frac{1}{2}$
∠HCA,因此∠1=∠2,同理可得,∠3=∠4,则∠1+∠3=∠2+∠4,即∠BAD=∠BCD,据此解答.
解答 解:如图所示:
因为EF∥GH,
所以∠EAC=∠HCA,∠FAC=∠GCA.
又因为AB,AD,CB,CD分别是∠EAC,∠FAC,∠GCA,∠HCA的平分线,
所以∠1=$\frac{1}{2}$∠EAC,∠2=$\frac{1}{2}$∠HCA,
所以∠1=∠2.
同理可得,∠3=∠4.
则∠1+∠3=∠2+∠4,
即∠BAD=∠BCD.
所以图中与∠BAD相等的角是∠BCD.
故答案为:∠BCD.
点评 本题考查了线段与角的综合,用到平行线的性质以及角平分线的定义等知识.


 阶梯计算系列答案
阶梯计算系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com