
分析 由题意知,把一批玩具的总数看作单位“1”,前两天完成的是总数的(1-$\frac{1}{3}$),则第一天完成的就是总数的(1-$\frac{1}{3}$)×$\frac{2}{2+7}$,第二天完成的是总数的(1-$\frac{1}{3}$)×$\frac{7}{2+7}$,已知第二天比第一天多做1000个,也就是多做了总数的[(1-$\frac{1}{3}$)×$\frac{7}{2+7}$-(1-$\frac{1}{3}$)×$\frac{2}{2+7}$],要求这批玩具共有多少个,就是求单位“1”的量是多少,根据分数除法的意义,列式解答即可.
解答 解:1000÷[(1-$\frac{1}{3}$)×$\frac{7}{2+7}$-(1-$\frac{1}{3}$)×$\frac{2}{2+7}$]
=1000÷[$\frac{14}{27}$-$\frac{4}{27}$]
=1000×$\frac{27}{10}$
=2700(个)
答:这批玩具共有2700个.
点评 解答本题的关键是,把两个不同的单位“1”转化成同一单位“1”,再利用“对应数÷对应分率=单位“1”的量”解答.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:小学数学 来源: 题型:填空题
查看答案和解析>>
科目:小学数学 来源: 题型:选择题
| A. | 70% | B. | 60% | C. | 28% | D. | 65% |
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:解答题
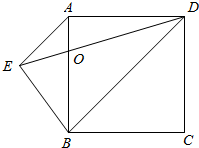 如图所示,ABCD是边长为12厘米的正方形,梯形AEBD的对角线相交于O,三角形AOE的面积比三角形BOD的面积小26平方厘米,梯形AEBD的面积是多少平方厘米?
如图所示,ABCD是边长为12厘米的正方形,梯形AEBD的对角线相交于O,三角形AOE的面积比三角形BOD的面积小26平方厘米,梯形AEBD的面积是多少平方厘米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com