Question

图中AB=AF，BC=CD，则∠DBF=

 

度．

Answer 1

考点：等腰三角形与等边三角形,角的度量

专题：平面图形的认识与计算

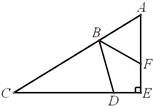
分析：如图：因为AB=AF，所以∠5=∠6；因为BC=CD，所以∠3=∠4；在三角形ACE中，∠E=90°，所以∠1+∠2=90°；因为三角形的内角和是180度，所以得出：∠2+∠5+∠6=180°，即∠2+2∠5=180°，∠1+∠3+∠4=180°，即∠1+2∠3=180°，则：∠1+2∠3+∠2+2∠5=360°，即：∠1+∠2+2（∠3+∠5）=360°，所以得出：∠3+∠5=135°，因为∠3、∠5和∠DBF组成了一个平角，进而用平角的度数-135°即可求出∠DBF的度数．

解答： 解：
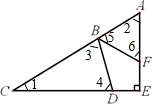
因为AB=AF，所以∠5=∠6；
因为BC=CD，所以∠3=∠4；
在三角形ACE中，∠E=90°，所以∠1+∠2=90°；
因为三角形的内角和是180度，所以得出：∠2+∠5+∠6=180°，即∠2+2∠5=180°①，
∠1+∠3+∠4=180°，即∠1+2∠3=180°②，
由①+②得：∠1+2∠3+∠2+2∠5=360°，即：
∠1+∠2+2（∠3+∠5）=360°，
所以得出：∠3+∠5=135°，
所以∠DBF=180°-（∠3+∠5）=180°-135°=45°；
故答案为：45．

点评：解答此题用到的知识点：（1）等腰三角形的特征；（2）三角形的内角和是180度；（3）平角的含义．