Question

8．找一找：如图所示：一张方桌可以坐4人

两张方桌这样拼起来，可以坐6人；照这样拼下去，5张方桌可以坐12人；n张桌子可以坐2n+2人． 16人需要7张方桌．

Answer 1

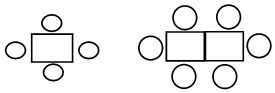
分析 观察摆放的桌子，不难发现：在1张桌子坐4人的基础上，多1张桌子，多2人．则有n张桌子时，有4+2（n-1）=2n+2人；由此即可计算当n=5求得人数，当2n+2=16人时，求得桌子张数n的值．

解答 解：第一张桌子可以坐4人；
拼2张桌子可以坐4+2×1=6人；
拼3张桌子可以坐4+2×2=8人；
…；
故n张桌子拼在一起可以坐4+2（n-1）=2n+2人．
5张方桌可以坐：2×5+2=12（人）；
当2n+2=16时，
   2n+2=16
       2n=14
        n=7，
答：5张方桌可以坐 12人；n张桌子可以坐 2n+2人． 16人需要 7张方桌．
故答案为：12，2n+2，7．

点评 此题考查了平面图形的规律变化，要求学生观察图形，分析、归纳并发现其中的规律，并应用规律解决问题．