
分析 第一次相遇时,两车共行一个全程,由于在距中点西侧10千米处相遇,所以相遇时快车比慢车多行了10×2=20千米,即每行一个全程,快车比慢车都要多行20千米,由于两车第二次相遇时,两车共行了3个全程,则两车第二次相遇时,快车比慢车多行了20×3=60千米,由于第二次相遇时距东站的距离占东西两站间距离的$\frac{3}{7}$,则此时快车距东站还有$\frac{3}{4}$个全程,慢车距西站还有1-$\frac{3}{7}$个全程,所以这60千米占全程的(1-$\frac{3}{7}$)-$\frac{3}{7}$个全程,则全程为:60÷[(1-$\frac{3}{7}$)-$\frac{3}{7}$].
解答 解:(10×2×3)÷[(1-$\frac{3}{7}$)-$\frac{3}{7}$]
=60÷[$\frac{4}{7}$-$\frac{3}{7}$]
=60÷$\frac{1}{7}$
=420(千米).
答:东西两站相距420千米.
点评 在此类相遇问题中,如果两车在距中点的n千米处相遇,则快车比慢车多行了2n千米.


 互动课堂系列答案
互动课堂系列答案科目:小学数学 来源: 题型:选择题
| A. | 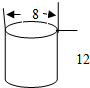 | B. | 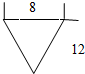 | C. |  | D. | 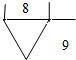 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com