
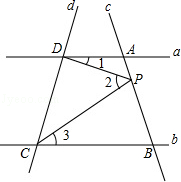
 如图,已知直线c和a、b分别交于A、B两点,点P在直线c上运动.
如图,已知直线c和a、b分别交于A、B两点,点P在直线c上运动.分析 (1)过点P作直线a的平行线,要想a∥b,两直线平行,那么过点P的直线必须和直线b也平行,两直线平行,内错角相等可知∠1+∠3=∠2;
(2)分两种情况,点P在点A上方,点P在点B下方,证明方法同第一问.
解答 解:(1)如图: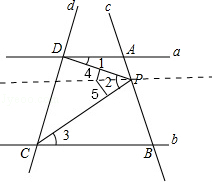
∠1+∠3=∠2时,a∥b
过点P作直线a的平行线,把∠2分成∠4和∠5
所以:
∠1=∠4
∠2=∠4+∠5
又因为:
∠2=∠1+∠3
所以:
∠5=∠3
所以:
过点P平行a的直线也平行于直线b
所以:
a∥b
(2)①当点P在点B的下方时,如图:
∠1=∠2+∠3时,a∥b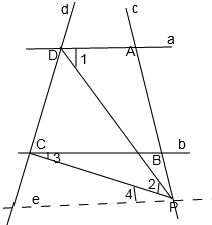
过点P作直线a的平行线e
所以:
∠1=∠2+∠4
因为:
∠1=∠2+∠3
所以:
∠3=∠4
所以:
b∥e
所以:
a∥b
如图:∠②当点P在点A的上方时,如图:
∠3=∠1+∠2时,a∥b
证明方法同上.
所以:∠3=∠1+∠2时,a∥b.
点评 此题考查平行线的判定和性质,关键是掌握内错角相等,两直线平行;两直线平行,内错角相等.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:小学数学 来源: 题型:填空题
查看答案和解析>>
科目:小学数学 来源: 题型:填空题
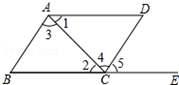 如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5;则一定能判定AB∥CD的条件有①、③、④(填写所有正确的序号).
如图,下列条件中:①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5;则一定能判定AB∥CD的条件有①、③、④(填写所有正确的序号).查看答案和解析>>
科目:小学数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com