
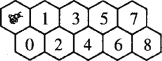
【题目】一排蜂房编号如图所示,左上角有一只小蜜蜂,还不会飞.只会向前爬行,它爬行到8号蜂房,共有________种路线.
【答案】55
【解析】
解法一、画树状图分析。

观察图形可以得出,共有55种不同的路线。
解法二、利用斐波那契数列解决。
按规则,蜜蜂从最初位置到0号蜂房只有唯一的一种爬法。从最初位置到1号蜂房有2种不同爬法:蜜蜂→1号;蜜蜂→0号→1号。同理,蜜蜂从最初位置到2号蜂房有3种不同爬法:蜜蜂→0号→2号;蜜蜂→1号→2号;蜜蜂→0号→1号→2号。从最初位置到3号蜂房有5种不同爬法:蜜蜂→1号→3号;蜜蜂→0号→2号→3号;蜜蜂→0号→1号→2号→3号;蜜蜂→1号→2号→3号;蜜蜂→0号→1号→3号。容易得出:蜜蜂要是想从最初位置爬到4号蜂房,那它在到4号蜂房之前,最后一个落脚点不是2号蜂房就是3号蜂房。所以蜜蜂从最初位置到4号蜂房的不同爬法的总数,就是它从最初位置到2号蜂房的不同爬法的总数与它从最初位置到3号蜂房的不同爬法的总数的和。因此蜜蜂从最初位置到4号蜂房的不同爬法的总数为3+5=8。以此类推,就会得到蜜蜂到达各蜂房的不同爬法总和分别是:1,2,3,5,8,13,21,34,55,89……
所以蜜蜂爬行到8号蜂房共有55种路线。


 名校课堂系列答案
名校课堂系列答案科目:小学数学 来源: 题型:
【题目】为配合市政府提出的“绿色出行,低碳生活”倡议,小枫和小楠就学校所在的社区开展了“我经常选择的出行方式”为主题的问卷调查(被调查者每人只能选择一种出行方式),并将调查结果分析整理后,做了下面两幅不完整的统计图.

请你结合图中所给出的信息解答下列问题
(1)小枫和小楠一共随机调查了多少人?
(2)选择其他出行方式的人数占总人数的百分之几?
(3)选择乘公共交通工具出行的有多少人?
(4)若该社区约有15000人,请你根据以上调查结果估计该社区有多少人会择乘公共交通工具出行?
查看答案和解析>>
科目:小学数学 来源: 题型:
【题目】如图是吴先生国庆节开车从深圳回老家F市的过程.下面说法,错误的是( )
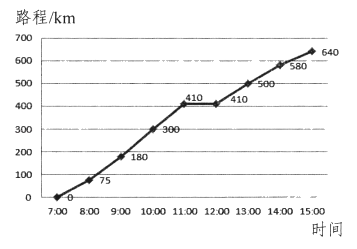
A.F市距离深圳640km
B.9:00﹣10:00车速最快
C.14:00﹣15:00行驶了60km
D.开车4小时后体息了20分钟
查看答案和解析>>
科目:小学数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,它们距A地的距离S与行驶时间t的关系如图所示,根据图象可知,甲车从B地返回的速度
为________千米/小时,甲车行驶到距A地________千米时追上乙车.

查看答案和解析>>
科目:小学数学 来源: 题型:
【题目】直接写出得数。
0.9×0.8= 0.8×1.2=
0.12×50= 60×0.8=
1.8×0.04= 0.15×0.4=
1.3×0.004= 5.8-0.8×5=
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com