
【题目】(4分)李刚骑自行车从甲地到乙地,要先骑一段上坡路,再骑一段平坦路,他到乙地后,立即返回甲地,来回共用了3小时.李刚在平坦路上比上坡路每小时多骑6千米,下坡路比平坦路每小时多骑3千米,还知道他在第1小时比第2小时少骑5千米,第2小时比第3小时少骑3千米.其中,第2小时骑了一段上坡路,又骑了一段平坦路,请问:
(1)李刚骑上坡路所用的时间是多少分钟?
(2)李刚骑下坡路所用的时间是多少分钟?
(3)甲、乙两地之间的距离是多少千米?
【答案】李刚骑上坡路所用的时间是70分钟,李刚骑下坡路所用的时间是40分钟,甲、乙两地之间的距离是22.5千米.
【解析】
试题分析:(1)设李刚在平路上骑车的速度为每小时x千米,则上坡时速度为每小时x﹣6千米,下坡时速度为每小时x+3千米,又设第二个小时内李刚上坡用了t小时,根据题意,可得(x﹣6)×1+5=(x﹣6)t+x(1﹣t),解得t=![]() ,则李刚上坡时间为(1+
,则李刚上坡时间为(1+![]() )×60=
)×60=![]() =70分钟,平路用了:60×2﹣70=50(分钟);又设第三个小时内李刚下坡用了m小时,则(x﹣6)×
=70分钟,平路用了:60×2﹣70=50(分钟);又设第三个小时内李刚下坡用了m小时,则(x﹣6)×![]() +x(1﹣
+x(1﹣![]() )+3=x(1﹣m)+(x+3)m,求出李刚第3个小时走下坡路和平坦路的时间即可;
)+3=x(1﹣m)+(x+3)m,求出李刚第3个小时走下坡路和平坦路的时间即可;
(2)根据上坡的路程与下坡的路程是相等的,可得(x﹣6)×![]() =(x+3)×
=(x+3)×![]() ,解得x=18千米;上坡时速度为每小时18﹣6=12千米,下坡时速度为每小时18+3=21千米,12×
,解得x=18千米;上坡时速度为每小时18﹣6=12千米,下坡时速度为每小时18+3=21千米,12×![]() +18×
+18×![]() +21×
+21×![]() =49千米,所以甲、乙两地之间的距离是:49÷2=22.5千米.
=49千米,所以甲、乙两地之间的距离是:49÷2=22.5千米.
解:设李刚在平路上骑车的速度为每小时x千米,
则上坡时速度为每小时x﹣6千米,下坡时速度为每小时x+3千米,
又设第二个小时内李刚上坡用了t小时,
根据题意,可得(x﹣6)×1+5=(x﹣6)t+x(1﹣t),
解得t=![]() ,
,
则李刚上坡时间为(1+![]() )×60=
)×60=![]() =70分钟,平路用了:60×2﹣70=50(分钟);
=70分钟,平路用了:60×2﹣70=50(分钟);
又设第三个小时内李刚下坡用了m小时,
则(x﹣6)×![]() +x(1﹣
+x(1﹣![]() )+3=x(1﹣m)+(x+3)m,
)+3=x(1﹣m)+(x+3)m,
解得m=![]() ,
,
得所以李刚下坡时间为:![]() =40分钟,平路用了:60﹣40=20(分钟);
=40分钟,平路用了:60﹣40=20(分钟);
综上,可得
(1)李刚骑上坡路所用的时间是70分钟,
(2)李刚骑下坡路所用的时间是40分钟,
根据上坡的路程与下坡的路程是相等的,
可得(x﹣6)×![]() =(x+3)×
=(x+3)×![]() ,
,
解得x=18千米;
因为上坡时速度为每小时18﹣6=12千米,下坡时速度为每小时18+3=21千米,
所以12×![]() +18×
+18×![]() +21×
+21×![]() =49千米,
=49千米,
则甲、乙两地之间的距离是:49÷2=22.5千米.
答:李刚骑上坡路所用的时间是70分钟,李刚骑下坡路所用的时间是40分钟,甲、乙两地之间的距离是22.5千米.


科目:小学数学 来源: 题型:
【题目】下图中每个小方格的边长是1cm,长方形ABCD的边已经画出两条。
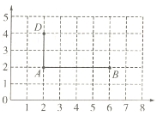
(1)点D的位置是(2,4),点A的位置是( ),点B的位置是( ),点C的位置是( )。
(2)求出这个长方形的面积。
(3)如果将长方形ABCD向上平移一格,那么平移后,这个长方形四个顶点的位置是A( ),B( ),C( ),D( )。
查看答案和解析>>
科目:小学数学 来源: 题型:
【题目】甲、乙、丙、丁四人玩扑克,发牌以后每人拿到13张牌(整副牌共52张).结果甲、乙两人共拿了11张黑桃.请问:丙、丁两人恰好每人拿到1张黑桃的概率是多少?有一人拿到2张黑桃,另一人没有拿到黑桃的概率又是多少?
查看答案和解析>>
科目:小学数学 来源: 题型:
【题目】一种礼品盒长5厘米,宽4厘米,高3厘米.乐乐想把这样的四个礼品盒包装成一个长方体.请算一算:怎样包装才能最省包装纸?最少需要多少平方厘米的包装纸?
查看答案和解析>>
科目:小学数学 来源: 题型:
【题目】
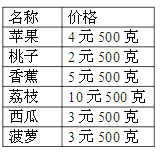
(1)苹果的价格是桃子的几倍?
(2)荔枝的价格是香蕉的几倍?
(3)买2千克菠萝需要多少钱?
(4)妈妈带了50元去买水果,买2500克苹果和1千克荔枝,够吗?如果够,还剩多少钱?
查看答案和解析>>
科目:小学数学 来源: 题型:
【题目】(8分)只列式不计算
(1)把5000元存入银行,定期2年,年利率2.74%,到期后扣除5%的利息税,实得利息多少元?
(2)某项目实际投资440万元,比计划多投入40万元,超支了百分之几?
(3)将35克盐加入165克水中,这种盐水的含盐率是多少?
(4)汽车从甲地开往乙地,1![]() 小时行了全程的
小时行了全程的![]() ,行完全程要多少小时?
,行完全程要多少小时?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com