
分析 改拼成一个每边比原来多一块的正方形,缺49块,所以32+49=81(块)正好拼满在首次拼成的大正方形的相邻两边周围,再减去相邻两边1个角上的地砖,等于首次拼成的大正方形边长的2倍,所以首次拼成的大正方形每边地砖数:(32+49-1)÷2=40(块).这批砖共有40×40+32,计算解决问题.
解答 解:原大正方形每边地砖有:
(32+49-1)÷2
=80÷2
=40(块)
这批砖原来有:
40×40+32
=1600+32
=1632(块)
答:这批砖原来有1632块.
点评 解决此题的关键是求出首次拼成的大正方形每边地砖数,然后求出这批砖的数量.


科目:小学数学 来源: 题型:解答题
查看答案和解析>>
科目:小学数学 来源: 题型:选择题
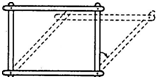 如图,用木条制成一个长方形框,其中长18厘米,宽15厘米.如果把它拉成平行四边形,周长和面积会怎样变化?( )
如图,用木条制成一个长方形框,其中长18厘米,宽15厘米.如果把它拉成平行四边形,周长和面积会怎样变化?( )| A. | 周长和面积都不变 | B. | 面积不变,周长变长 | ||
| C. | 面积变小,周长不变 | D. | 面积变大,周长不变 |
查看答案和解析>>
科目:小学数学 来源: 题型:计算题
| 120÷6= | 30×10= | 3000÷5= | 12×0= | 505÷5= |
| 960÷3= | 69÷3= | 90×50= | 0÷2= | 40×11= |
| 148÷5≈ | 602÷6≈ | 570÷8≈ | 311÷4≈ | 134÷7≈ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com