Question

13．小明拿了两个一样的等腰直角三角尺拼成了下面的图形，你能算出两块三角尺重合部分（阴影部分）的面积吗？

Answer 1

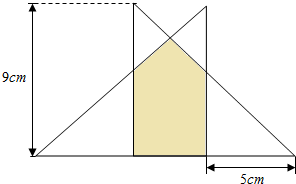
分析 由图可知，阴影部分的面积可看作大直角三角形的面积减去本三角形内两个小直角三角形的面积．因为△ADE与△CHG全等，所以AD=DE=CG=5（厘米），EF=DF-DE=9-5=4（厘米）；运用面积公式可以求出各三角形的面积，解决问题．

解答 解：如图：因为△ADE与△CHG全等，所以AD=DE=CG=5（厘米），EF=DF-DE=9-5=4（厘米）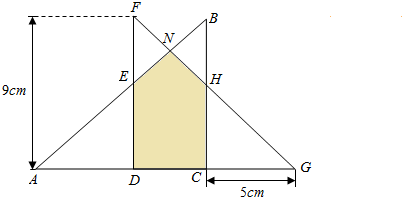

两块三角尺重合部分（阴影部分）的面积：
$\frac{1}{2}$×9×9-$\frac{1}{2}$×5×5-$\frac{1}{2}$×（9-5）×（9-5）×$\frac{1}{2}$
=40.5-12.5-4
=24（平方厘米）．
答：两块三角尺重合部分（阴影部分）的面积是24平方厘米．

点评 此题解答的关键在于看清楚阴影部分的面积由哪几个三角形的面积差构成，进而得解．