
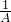 +
+ =
= .则A-B=________.
.则A-B=________.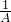 +
+ =
= ,可知
,可知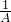
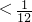 ,
, <
< ,即A>12,B>12,又因A>B,可知B是一个大于13且小于32的自然数,然后分情况讨论,可分别求出A、B的值,据此解答.
,即A>12,B>12,又因A>B,可知B是一个大于13且小于32的自然数,然后分情况讨论,可分别求出A、B的值,据此解答.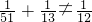 ,
,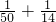 ≠
≠ ,
,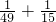 ≠
≠ ,
,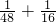 =
= ,
,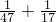 ≠
≠ ,
,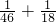 ≠
≠ ,
,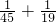 ≠
≠ ,
,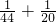 ≠
≠ ,
,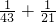 ≠
≠ ,
,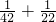 ≠
≠ ,
, ≠
≠ ,
,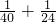 ≠
≠ ,
,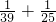 ≠
≠ ,
,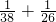 ≠
≠ ,
,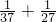 ≠
≠ ,
, ≠
≠ ,
,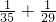 ≠
≠ ,
,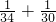 ≠
≠ ,
, ≠
≠ ,
,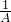 +
+ =
= .
.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com