
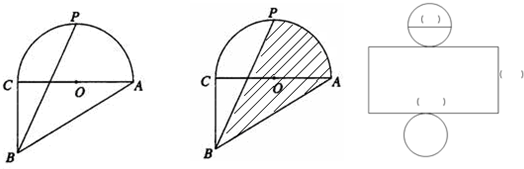
分析 (1)利用圆的对称性可知:两个阴影部分面积相等(OC=OA;CD=EA;OD=OE)
等底同高的三角形面积相等 所以 S△POD=S△POE;S△CDB=S△AEB;S△BOD=S△BOE;
于是:S△BOP=S△POD+S△BOD=S△POE+S△BOE,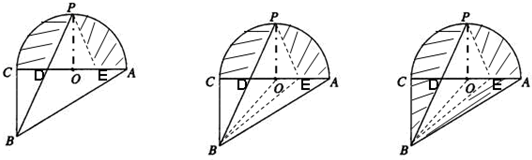
根据题意阴影部分的面积与空白部分面积的差为16,即为三角形PEB的面积是16,据此解答即可.
(2)根据第一问求得的数据可知,d=4,c=长方形的长=πd=3.14×4=12.56,再根据长方形的长与宽之比为3.14:1求得长方形的宽是12.56÷3.14=4.
(3)根据圆柱的体积V=sh解答即可.
解答 解:如图,利用圆的对称性可知:两个阴影部分面积相等(OC=OA;CD=EA;OD=OE)
等底同高的三角形面积相等 所以 S△POD=S△POE;S△CDB=S△AEB;S△BOD=S△BOE;
于是:S△BOP=S△POD+S△BOD=S△POE+S△BOE
因此 原图中阴影部分与空白部分的面积差就转化为三角形PBE的面积了,
则有:2S△BOP=16
所以:
$2×\frac{1}{2}OP•OC=16$
OP=OC=4
即小圆的直径为4.
(2)3.14×4=12.56
12.56÷3.14=4
答:小圆直径处填4,长方形的长是12.56,长方形的宽是4.
故答案为:4,12.56,4.
(3)3.14×(4÷2)2×4
=3.14×16
=50.24
答:圆柱的体积是50.24.
点评 解决此题的关键是做出合适的辅助线,将图形进行相应转换,利用已知条件求得阴影部分的面积.


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com