考点:圆锥的体积,圆柱的侧面积、表面积和体积
专题:立体图形的认识与计算
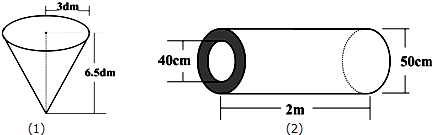
分析:(1)圆锥的底面半径和高已知,利用圆锥的体积V=
Sh,即可求出这个圆锥的体积.
(2)此题也可以利用圆环柱的体积V=(S
外-S
内)h进行计算,先求出底面的面积,也就是圆环的面积,用大圆的面积减小圆的面积就是圆环的面积,再乘高即可.
解答:
解:(1)
×3.14×3
2×6.5
=3.14×19.5
=61.23(立方分米)
答:圆锥的体积是61.23立方分米.
(3)50÷2=25(厘米)
40÷2=20(厘米)
2米=200厘米
3.14×(25
2-20
2)×200
=3.14×(625-400)×200
=3.14×225×200
=141300(立方厘米)
答:这个管道的体积是141300立方厘米.
故答案为:61.23立方分米,141300立方厘米.
点评:此题主要考查长方体的表面积和圆锥、圆柱的体积的计算方法.



 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案