练习册

  • 练习册
  • 试题
    精英家教网 > 小学数学 > 题目详情
    9．用三根相同的绳子分别围成圆形、正方形、长方形，圆的面积最大．√．（判断对错）

    分析 我们假设绳子的长度是20，因此正方形的边长就是20÷4=5，进一步求出正方形的面积；长方形的长与宽的和就是20÷2=10，令长方形的长是6宽是4，然后求出长方形的面积；运用公式求出半径，进一步求出圆的面积，通过面积的比较再作出选择．

    解答 解：正方形的面积：
    20÷4=5，
    5×5=25；

    长方形的面积：
    20÷2=10，

    假设长是6，宽是4，
    6×4=24，
    3.14×（20÷3.14÷2）2，
    ≈3.14×32，
    =28.26，
    因此圆的面积最大，长方形的面积最小．
    故答案为：√．

    点评 本题运用长方形、正方形和圆的面积公式进行计算即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：小学数学 来源： 题型：填空题

    19．如果9x=4y，那么x：y=4：9．

    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

    20．一个平行四边形的面积是4.2平方厘米，高1.4厘米，则底是3厘米．

    查看答案和解析>>

    科目：小学数学 来源： 题型：解答题

    17．上午8：30，小明骑自行车从家出发，8分钟后，爸爸骑摩托车去追他，在离家4千米的地方追上他，然后爸爸立即回家．到家后又立即回头去追小明．再追上他的时候，离家恰好是8千米，这时是几点几分？

    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

    4．如果把2.6升的饮料倒入200亳升的量杯内，最多可以倒满13杯．

    查看答案和解析>>

    科目：小学数学 来源： 题型：解答题

    14．探究分析
    我们已经知道三角形的内角和是180°，我们可以用这个知识求出四边形、五边形、六边形内角和的度数，进而探索出多边形的内角和．
    多    边    形内角和的度数
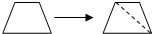    180°×2=360°
    180°×3=540°
    ①阅读表格中的内容并填空．
    ②根据四边形、五边形、六边形内角和的计算方法，归纳出n边形的内角和：n边形的内角和=180°（n-2）（用含有字母n的式子表示）．
    ③若某多边形的内角和是1440°，利用前面探究的结论计算这个多边形的边数．

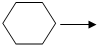    查看答案和解析>>

    科目：小学数学 来源： 题型：选择题

    1．一件衣服，老板在进价的基础上增加20%挂牌出售．一位顾客通过还价，八折购得这件衣服，你认为这个老板（　　）
    A．赚钱了B．赔钱了C．不赔不赚D．无法确定

    查看答案和解析>>

    科目：小学数学 来源： 题型：解答题

    18．学校体育室买了8个篮球和12个排球，已知每个篮球128元，每个排球72元，一共需付多少元．

    查看答案和解析>>

    科目：小学数学 来源： 题型：填空题

    19．4吨煤，用去$\frac{1}{2}$吨后还剩2吨．×（判断对错）

    查看答案和解析>>

    同步练习册答案