
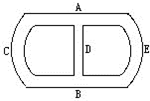
 如图是一个跑道的示意图,沿ACBEA走一圈是400米,沿ACBDA走一圈是275米,其中A到B的直线距离是75米.甲、乙二人同时从A点出发练长跑,甲沿ACBDA的小圈跑,每100米用24秒,乙沿ACBEA的大圈跑,每100米用21秒.问:
如图是一个跑道的示意图,沿ACBEA走一圈是400米,沿ACBDA走一圈是275米,其中A到B的直线距离是75米.甲、乙二人同时从A点出发练长跑,甲沿ACBDA的小圈跑,每100米用24秒,乙沿ACBEA的大圈跑,每100米用21秒.问:| 25 |
| 6 |
| 100 |
| 21 |
| 25 |
| 42 |
| 25 |
| 6 |
| 100 |
| 21 |
| 100 |
| 21 |
| 25 |
| 42 |
| 25 |
| 6 |


科目:小学数学 来源: 题型:
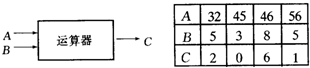
 如图是一个运算器的示意图,A、B是输入的两个数据,C是输出的结果.下表是输入A、B数据后,运算器输出C的对应值.请你据此判断,当输入A值是1999,输入B值是9时,运算器输出的C是
如图是一个运算器的示意图,A、B是输入的两个数据,C是输出的结果.下表是输入A、B数据后,运算器输出C的对应值.请你据此判断,当输入A值是1999,输入B值是9时,运算器输出的C是| A | 32 | 45 | 46 | 56 |
| B | 5 | 3 | 8 | 5 |
| C | 2 | 0 | 6 | 1 |
查看答案和解析>>
科目:小学数学 来源: 题型:
查看答案和解析>>
科目:小学数学 来源: 题型:填空题
 如图是一个瓶子的示意图,瓶子的底面半径是4cm,将它正放时,瓶中饮料的高度是15cm,倒放时,空余部分的高度是10cm,这个甁子的容积是________.
如图是一个瓶子的示意图,瓶子的底面半径是4cm,将它正放时,瓶中饮料的高度是15cm,倒放时,空余部分的高度是10cm,这个甁子的容积是________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com