
 ①如图,9个3×3的小方格表合并成一个9×9的大方格表,每个格子中填入1-9中的一个数,每个数在每一行、每一列中都只出现一次,并且在原来的每个3×3的小方格表中也只出现一次,10个“☆”处所填数的总和是
①如图,9个3×3的小方格表合并成一个9×9的大方格表,每个格子中填入1-9中的一个数,每个数在每一行、每一列中都只出现一次,并且在原来的每个3×3的小方格表中也只出现一次,10个“☆”处所填数的总和是


科目:小学数学 来源: 题型:
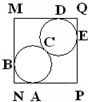 如图,两个完全相同的圆相切,都与圆外边的正方形PQMN相切,共有5五个切点A、B、C、D、E,将1~9这九个数字分别放在这五个切点和正方形四个顶点上,使正方形每边上的三个数的和均为质数,则A、B、C、、D、E、M、N、Q、P对应的数分别为
如图,两个完全相同的圆相切,都与圆外边的正方形PQMN相切,共有5五个切点A、B、C、D、E,将1~9这九个数字分别放在这五个切点和正方形四个顶点上,使正方形每边上的三个数的和均为质数,则A、B、C、、D、E、M、N、Q、P对应的数分别为查看答案和解析>>
科目:小学数学 来源: 题型:
 如图,9个3×3的小方格表合并成一个9×9的大方格表,每个格子中填入1-9中的一个数,每个数在每一行、每一列中都只出现一次,并且在原来的每个3×3的小方格表中也只出现一次,10个“☆”处所填数的总和是
如图,9个3×3的小方格表合并成一个9×9的大方格表,每个格子中填入1-9中的一个数,每个数在每一行、每一列中都只出现一次,并且在原来的每个3×3的小方格表中也只出现一次,10个“☆”处所填数的总和是查看答案和解析>>
科目:小学数学 来源: 题型:
 如图所示的9个圆圈在4个小的等边三角形和3个大的等边三角形的顶点处,在图上将1~9这9个数字填入圆圈,要求这7个三角形中每个三角形3个顶点上的数字之和都相等.
如图所示的9个圆圈在4个小的等边三角形和3个大的等边三角形的顶点处,在图上将1~9这9个数字填入圆圈,要求这7个三角形中每个三角形3个顶点上的数字之和都相等.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com