
 如图A、B分别是长方形长和宽的中点,阴影部分的面积是长方形的
如图A、B分别是长方形长和宽的中点,阴影部分的面积是长方形的


 b,三角形2的底和高分别是
b,三角形2的底和高分别是 a和
a和 b,三角形3的底和高分别是 b和
b,三角形3的底和高分别是 b和 a,根据三角形的面积公式能算出3个空白三角形部分的面积,则阴影部分的面积=长方形的面积-空白部分的面积,从而找出阴影部分的面积与长方形的面积的百分比.
a,根据三角形的面积公式能算出3个空白三角形部分的面积,则阴影部分的面积=长方形的面积-空白部分的面积,从而找出阴影部分的面积与长方形的面积的百分比. 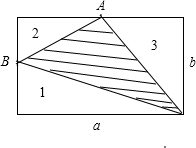
 ×a×
×a× b,
b, ab,
ab, ×
× a×
a× b,
b, ab,
ab, ×
× a×b,
a×b, ab,
ab, ab+
ab+ ab+
ab+ ab,
ab, ab,
ab, ab,
ab, ab,
ab, ab÷ab=
ab÷ab= ,
, .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com